
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段EF的长为( )
,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段EF的长为( )

A.![]() B.
B.![]() C.4D.
C.4D.![]()
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,点E在AD上,请仅用无刻度直尺按要求作图(保留作图痕迹,不写作法)
(1)在图1中,过点E作直线EF将□ABCD分成两个全等的图形;
(2)在图2中,DE=DC,请你作出∠BAD的平分线AM.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图8,AB两地之间有一座山,以前从A地到B地需要经过C地.现在政府出资打通了一条山岭隧道,使从A地到B地可沿直线AB直接到达.已知BC=8km,∠A=45°,∠B=53°.
(1)求点C到直线AB的距离;
(2)求现在从A地到B地可比原来少走多少路程?(结果精确到0.1km;参考数据:![]() ≈1.41,sin53°≈0.80,cos53°≈0.60)
≈1.41,sin53°≈0.80,cos53°≈0.60)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是边长为12 cm的正三角形,动点P从A向B以2 cm/s匀速运动,同时动点Q从B向C以1 cm/s匀速运动,当点P到达点B时,P,Q两点停止运动,设点P的运动时间为t秒,则当△PBQ为直角三角形时,t的值为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:有一个角是其邻角一半的圆内接四边形叫做圆内倍角四边形.
(1)如图1,四边形ABCD内接于⊙O,∠DCB﹣∠ADC=∠A,求证:四边形ABCD为圆内接倍角四边形;
(2)在(1)的条件下,⊙O半径为5.
①若AD为直径,且sinA=![]() ,求BC的长;
,求BC的长;
②若四边形ABCD中有一个角为60°,且BC=CD,则四边形ABCD的面积是 ;
(3)在(1)的条件下,记AB=a,BC=b,CD=c,AD=d,求证:d2﹣b2=ab+cd.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A的坐标为![]() .
.
(1)如图1,若点B 在x轴正半轴上,点![]() ,
,![]() ,
,![]() ,求点B坐标;
,求点B坐标;
(2)如图2,若点B 在x轴负半轴上,![]() 轴于点E,
轴于点E,![]() 轴于点F,
轴于点F,![]() ,MF交直线AE于点M,若点
,MF交直线AE于点M,若点![]() ,BM=5,求点M坐标.
,BM=5,求点M坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB是⊙O的直径,弦CD⊥AB于H,过CD延长线上一点E作⊙O的切线交AB的延长线于F,切点为G,连接AG交CD于K.
(1)如图1,求证:KE=GE;
(2)如图2,连接CABG,若∠FGB=![]() ∠ACH,求证:CA∥FE;
∠ACH,求证:CA∥FE;
(3)如图3,在(2)的条件下,连接CG交AB于点N,若sinE=![]() ,AK=
,AK=![]() ,求CN的长.
,求CN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】BD、CE分别是△ABC的边AC、AB上的高,P在BD的延长线上,且BP=AC,点Q在CE上,CQ=AB,
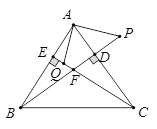
求证:(1)AP=AQ ;
(2)AP⊥AQ.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com