
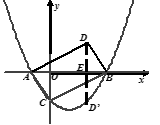
【题目】如图,抛物线y=x2-x+a与x轴交于点A,B,与y轴交于点C,其顶点在直线y=-2x上.
【1】求a的值;
【2】求A,B的坐标;
【3】以AC,CB为一组邻边作□ACBD,则点D关于x轴的对称点D′ 是否在该抛物线上?请说明理由.

【答案】
【1】抛物线的顶点坐标为(1,a-)
∵顶点在直线y=-2x上,∴a-=-2.即a=-
【2】由(1)知,抛物线表达式为y=x2-x- ,
令y=0,得x2-x- =0.解之得:x1=-1,x3=3.
∴A的坐标 (-1,0),B的坐标 (3,0);
【3】∵四边形ABCD是平行四边形,
∴点C,D关于对角线交点(1,0)对称又∵点D′ 是点D关于x轴的对称点,点C,D′ 关于抛物线的对称轴对称.∴D′ 在抛物线上.
【解析】(1)根据抛物线的顶点在直线y=-2x上,运用待定系数法求得
(2)由(1)得抛物线的解析式,因为A,B的坐标在x轴上,所以纵坐标为0,代入抛物线的解析式,解一元二次方程可求得A,B的坐标
(3)由平行四边形知C,D关于对角线交点对称,通过点D′ 是点D关于x轴的对称点,可知点C,D′ 关于抛物线的对称轴对称,即可得出结论


科目:初中数学 来源: 题型:
【题目】“一带一路”是“丝绸之路经济带”和“21世纪海上丝绸之路”的简称.旨在借用古代丝绸之路的历史符号,高举和平发展的旗帜,积极发展与沿线国家的经济合作.2018年底共开行中欧班列6300列,其中返程班列2690列,实现进出口贸易总额170亿美元.数据170亿用科学计数法表示为![]() ,则
,则![]() 的值为( )
的值为( )
A.9B.10C.11D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
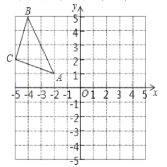
【题目】由边长为1的小正方形组成的格点中,建立如图平面直角坐标系,△ABC的三个顶点坐标分别为A(2,1),B(4,5),C(5,2).
(1)请画出△ABC关于y轴对称的△A![]() B
B![]() C
C![]() ;
;
(2)画出△ABC关于原点O成中心对称的△A![]() B
B![]() C
C![]() ;
;
(3)请你判断△AA![]() A
A![]() 与△CC
与△CC![]() C
C![]() 的相似比;若不相似,请直接写出△AA
的相似比;若不相似,请直接写出△AA![]() A
A![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 轴上,已知点
轴上,已知点![]() 的坐标为
的坐标为![]() ,且
,且![]() .
.
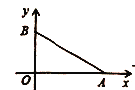
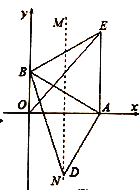
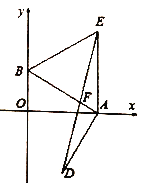
(1) (2) (3)
(1)求![]() 的长度;
的长度;
(2)以![]() 为一边作等边,过点
为一边作等边,过点![]() 作
作![]() ,交
,交![]() 的垂直平分线
的垂直平分线![]() 于点
于点![]() .求证:
.求证:![]() ;
;
(3)在(2)的条件下,连接![]() 交
交![]() 于
于![]() ,求证:
,求证:![]() 为
为![]() 的中点.
的中点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一工地计划租用甲、乙两辆车清理淤泥,从运输量来估算:若租两车合运,10天可以完成任务;若单独租用乙车完成任务则比单独租用甲车完成任务多用15天.
(1)甲、乙两车单独完成任务分别需要多少天?
(2)已知两车合运共需租金65000元,甲车每天的租金比乙车每天的租金多1500元,试问:租甲乙两车、单独租甲车、单独租乙车这三种租车方案中,哪一种租金最少?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《代数学》中记载,形如x2+10x=39的方程,求正数解的几何方法是:“如图1,先构造一个面积为x2的正方形,再以正方形的边长为一边向外构造四个面积为![]() x的矩形,得到大正方形的面积为39+25=64,则该方程的正数解为8-5=3”,小聪按此方法解关于x的方程x2+6x+m=0时,构造出如图2所示的图形,己知阴影部分的面积为36,则该方程的正数解为( )
x的矩形,得到大正方形的面积为39+25=64,则该方程的正数解为8-5=3”,小聪按此方法解关于x的方程x2+6x+m=0时,构造出如图2所示的图形,己知阴影部分的面积为36,则该方程的正数解为( )

A.6B.3![]() -3C.3
-3C.3![]() -2D.3
-2D.3![]() -
-![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校实施新课程改革以来,学生的学习能力有了很大提高,王老师为进一步了解本班学生自主学习、合作交流的现状,对该班部分学生进行调查,把调查结果分成四类(A:特别好,B:好,C:一般,D:较差)后,再将调查结果绘制成两幅不完整的统计图(如图①②).请根据统计图解答下列问题:
(1)本次调查中,王老师一共调查了________名学生;
(2)将条形统计图补充完整;
(3)为了共同进步,王老师从被调查的A类和D类学生中分别选取一名学生进行“兵教兵”互助学习,请用列表或画树状图的方法求出恰好选中一名男生和一名女生的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】.如图,在平面直角坐标系xOy中,直线y=kx+b(k≠0)与双曲线![]() 相交于点A(m,3),B(-6,n),与x轴交于点C.
相交于点A(m,3),B(-6,n),与x轴交于点C.
(1)求直线y=kx+b(k≠0)的解析式;
(2)若点P在x轴上,且S△ACP=![]() S△BOC,求点P的坐标(直接写出结果).
S△BOC,求点P的坐标(直接写出结果).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图 ,在平行四边形 ABCD 中,对角线 AC 、 BD 交于点 O ,并且 DAC 60 ,ADB 15 ,点 E 是 AD 上一动点,延长 EO 交 BC 于点 F 。当点 E 从 D 点向 A 点移动 过程中(点 E 与点 D 、点 A 不重合),则四边形 AFCE 的变化是( )
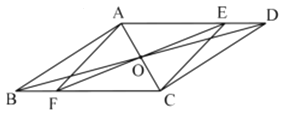
A.平行四边形→矩形→平行四边形→菱形→平行四边形
B.平行四边形→矩形→平行四边形→正方形→平行四边形
C.平行四边形→菱形→平行四边形→矩形→平行四边形
D.平行四边形→矩形→菱形→正方形→平行四边形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com