
分析 (1)根据分式的分子分母都乘以(或除以)同一个不为零的整式,分式的值不变,可得答案;
(2)根据分式的除法:除以一个分式等于乘以这个分式的倒数,可得答案.
解答 解:(1)$\frac{4a{b}^{3}{c}^{2}}{6{a}^{2}{b}^{3}c}$=$\frac{2c}{3a}$,
(2)$\frac{{x}^{2}+2x+1}{{x}^{2}-4}$÷$\frac{x+1}{x-2}$=$\frac{(x+1)^{2}}{(x+2)(x-2)}$•$\frac{x-2}{x+1}$=$\frac{x+1}{x+2}$,
故答案为:$\frac{2c}{3a}$,$\frac{x+1}{x+2}$.
点评 本题考查了分式的性质,利用了分式的性质,分式的除法.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
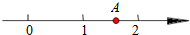 如图所示,在数轴上点A所表示的数x的范围是( )
如图所示,在数轴上点A所表示的数x的范围是( )| A. | $\frac{3}{2}$sin30°<x<sin60° | B. | cos30°<x<$\frac{3}{2}$cos45° | ||
| C. | $\frac{3}{2}$tan30°<x<tan45° | D. | $\frac{3}{2}$tan45°<x<tan60° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com