【题目】如图，使ΔABC≌ΔADC成立的条件是（ ）
A.AB=AD，∠B=∠DB.AB=AD，∠ACB=ACD
C.BC=DC，∠BAC=∠DACD.AB=AD，∠BAC=∠DAC
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系中，△ABC的三个顶点的位置如图所示，点A'的坐标是（－2，2），现将△ABC平移，使点A变换为A'，点B'、C'分别是点B、C的对应点．
（1）请画出平移后的△A'B'C'（不写画法），并直接写出点B'、C'的坐标：B'_________，C'_________；
（2）若△ABC内部一点P的坐标为（a，b），则点P的对应点P'的坐标是____________ ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】知识背景
当a＞0且x＞0时，因为（
﹣
）2≥0，所以x﹣2
+
≥0，从而x+
（当x=时取等号）．
设函数y=x+（a＞0，x＞0），由上述结论可知：当x=时，该函数有最小值为2．
应用举例
已知函数为y1=x（x＞0）与函数y2=
（x＞0），则当x=
=2时，y1+y2=x+有最小值为2=4．
解决问题
（1）已知函数为y1=x+3（x＞﹣3）与函数y2=（x+3）2+9（x＞﹣3），当x取何值时，
有最小值？最小值是多少？
（2）已知某设备租赁使用成本包含以下三部分：一是设备的安装调试费用，共490元；二是设备的租赁使用费用，每天200元；三是设备的折旧费用，它与使用天数的平方成正比，比例系数为0.001．若设该设备的租赁使用天数为x天，则当x取何值时，该设备平均每天的租货使用成本最低？最低是多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】等边三角形ABC 中，BD是角平分线，点E在BC边的延长线上，且CD=CE，则∠BDE的度数是（ ）
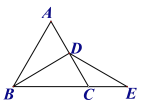
A.90°B.100°C.120°D.无法确定
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在半径为4的⊙O中，CD为直径，AB⊥CD且过半径OD的中点，点E为⊙O上一动点，CF⊥AE于点F.当点E从点B出发顺时针运动到点D时，点F所经过的路径长为( )
A. 
π B. 
π C. 
π D. 
π
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】列方程解应用题：某商场经市场调查，预计一款夏季童装能获得市场青睐，便花费15000元购进了一批此款童装，上市后很快售罄．该店决定继续进货，由于第二批进货数量是第一批进货数量的2倍，因此单价便宜了10元，购进第二批童装一共花费了27000元．那该店所购进的第一批童装的价格是多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】抛物线
上部分点的横坐标x，纵坐标y的对应值如下表：
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
y | … | 0 | 4 | 6 | 6 | 4 | … |
从上表可知，下列说法正确的个数是（ ）
①抛物线与x轴的一个交点为（﹣2，0）；②抛物线与y轴的交点为（0，6）；
③抛物线的对称轴是x=1；④在对称轴左侧y随x增大而增大．
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知等腰△ABC中，AB=AC，∠BAC=120°，AD⊥BC于点D，点P是BA延长线上一点，点O是线段AD上一点，OP=OC，下面的结论： ①∠APO+∠DCO=30°；②△OPC是等边三角形；③AC=AO+AP；④S△ABC=S四边形AOCP，其中正确的个数是（ ）
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在边长为
的菱形
中，对角线
，点
是直线
上的动点，
于
，
于
．
如图，在边长为的菱形中，对角线，点是直线上的动点，于，于．
对角线
的长是________，菱形的面积是________；
如图
，当点在对角线上运动时，
的值是否发生变化？请说明理由；
如图
，当点在对角线的延长线上时，的值是否发生变化？若不变请说明理由，若变化，请直接写出
、
之间的数量关系，不用明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
