
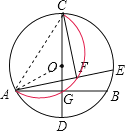
【题目】如图,在半径为4的⊙O中,CD为直径,AB⊥CD且过半径OD的中点,点E为⊙O上一动点,CF⊥AE于点F.当点E从点B出发顺时针运动到点D时,点F所经过的路径长为( )

A. ![]() π B.
π B. ![]() π C.
π C. ![]() π D.
π D. ![]() π
π
【答案】D
【解析】
连接AC,AO,由AB⊥CD,利用垂径定理得到G为AB的中点,由中点的定义确定出OG的长,在直角三角形AOG中,由AO与OG的长,利用勾股定理求出AG的长,进而确定出AB的长,由CO+GO求出CG的长,在直角三角形AGC中,利用勾股定理求出AC的长,由CF垂直于AE,得到三角形ACF始终为直角三角形,点F的运动轨迹为以AC为直径的半径,如图中红线所示,当E位于点B时,CG⊥AE,此时F与G重合;当E位于D时,CA⊥AE,此时F与A重合,可得出当点E从点B出发顺时针运动到点D时,点F所经过的路径长![]() ,在直角三角形ACG中,利用锐角三角函数定义求出∠ACG的度数,进而确定出
,在直角三角形ACG中,利用锐角三角函数定义求出∠ACG的度数,进而确定出![]() 所对圆心角的度数,再由AC的长求出半径,利用弧长公式即可求出
所对圆心角的度数,再由AC的长求出半径,利用弧长公式即可求出![]() 的长,即可求出点F所经过的路径长.
的长,即可求出点F所经过的路径长.
连接AC,AO,
∵AB⊥CD,
∴G为AB的中点,即AG=BG=![]() AB,
AB,
∵⊙O的半径为4,弦AB⊥CD且过半径OD的中点,
∴OG=2,
∴在Rt△AOG中,根据勾股定理得:AG=![]() =2
=2![]() ,
,
∴AB=2AG=4![]() ,
,
又∵CG=CO+GO=4+2=6,
∴在Rt△AGC中,根据勾股定理得:AC=![]() ,
,
∵CF⊥AE,
∴△ACF始终是直角三角形,点F的运动轨迹为以AC为直径的半圆,
当E位于点B时,CG⊥AE,此时F与G重合;当E位于D时,CA⊥AE,此时F与A重合,
∴当点E从点B出发顺时针运动到点D时,点F所经过的路径长![]() ,
,
在Rt△ACG中,tan∠ACG=![]() ,
,
∴∠ACG=30°,
∴![]() 所对圆心角的度数为60°,
所对圆心角的度数为60°,
∵直径AC=4![]() ,
,
∴![]() 的长为
的长为![]() =
=![]() ,
,
则当点E从点B出发顺时针运动到点D时,点F所经过的路径长为![]() .
.
故选D.


 学业测评一课一测系列答案
学业测评一课一测系列答案科目:初中数学 来源: 题型:
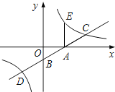
【题目】正方形A1B1C1O ,A2B2C2C1,A3B3C3C2 … 按如图的方式放置点A1 ,A2 ,A3和点C1 ,C2 ,C3 …分别在直线y=x+1和x轴上,则点B2019的纵坐标是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
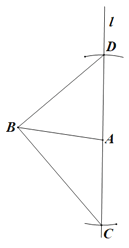
【题目】在一次研究性学习活动中,同学们看到了工人师傅在木板上画一个直角三角形的过程(如图所示):画线段AB,过点A任作一条直线l,以点A为圆心,以AB长为半径画弧,与直线l相交于两点C、D,连接BC和BD.则△BCD就是直角三角形.
(1)请你说明△BCD是直角三角形的道理;
(2)请利用上述方法作一个直角三角形,使其中一个锐角为60°(不写作法,保留作图
痕迹,在图中注明60°的角).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一种实验用轨道弹珠,在轨道上行驶5分钟后离开轨道,前2分钟其速度v(米/分)与时间t(分)满足二次函数v=at2,后三分钟其速度v(米/分)与时间t(分)满足反比例函数关系,如图,轨道旁边的测速仪测得弹珠1分钟末的速度为2米/分,求:
(1)二次函数和反比例函数的关系式.
(2)弹珠在轨道上行驶的最大速度.

【答案】(1)v=![]() (2<t≤5) (2)8米/分
(2<t≤5) (2)8米/分
【解析】分析:(1)由图象可知前一分钟过点(1,2),后三分钟时过点(2,8),分别利用待定系数法可求得函数解析式;
(2)把t=2代入(1)中二次函数解析式即可.
详解:(1)v=at2的图象经过点(1,2),
∴a=2.
∴二次函数的解析式为:v=2t2,(0≤t≤2);
设反比例函数的解析式为v=![]() ,
,
由题意知,图象经过点(2,8),
∴k=16,
∴反比例函数的解析式为v=![]() (2<t≤5);
(2<t≤5);
(2)∵二次函数v=2t2,(0≤t≤2)的图象开口向上,对称轴为y轴,
∴弹珠在轨道上行驶的最大速度在2秒末,为8米/分.
点睛:本题考查了反比例函数和二次函数的应用.解题的关键是从图中得到关键性的信息:自变量的取值范围和图象所经过的点的坐标.
【题型】解答题
【结束】
24
【题目】阅读材料:小胖同学发现这样一个规律:两个顶角相等的等腰三角形,如果具有公共的顶角的顶点,并把它们的底角顶点连接起来则形成一组旋转全等的三角形.小胖把具有这个规律的图形称为“手拉手”图形.如图1,在“手拉手”图形中,小胖发现若∠BAC=∠DAE,AB=AC,AD=AE,则BD=CE.
(1)在图1中证明小胖的发现;
借助小胖同学总结规律,构造“手拉手”图形来解答下面的问题:
(2)如图2,AB=BC,∠ABC=∠BDC=60°,求证:AD+CD=BD;
(3)如图3,在△ABC中,AB=AC,∠BAC=m°,点E为△ABC外一点,点D为BC中点,∠EBC=∠ACF,ED⊥FD,求∠EAF的度数(用含有m的式子表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() ,
,![]() 轴分别交于点
轴分别交于点![]() ,
,![]() ,与反比例函数
,与反比例函数![]() 图象交于点
图象交于点![]() ,
,![]() ,过点
,过点![]() 作
作![]() 轴的垂线交该反比例函数图象于点
轴的垂线交该反比例函数图象于点![]() .
.
![]() 求点
求点![]() 的坐标.
的坐标.
![]() 若
若![]() .
.
①求![]() 的值.
的值.
②试判断点![]() 与点
与点![]() 是否关于原点
是否关于原点![]() 成中心对称?并说明理由.
成中心对称?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,使ΔABC≌ΔADC成立的条件是( )

A.AB=AD,∠B=∠DB.AB=AD,∠ACB=ACD
C.BC=DC,∠BAC=∠DACD.AB=AD,∠BAC=∠DAC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2的图象与一次函数y=mx+4的图象相交于点A(-2,2)和B(n,8)两点.
(1)求二次函数y=ax2与一次函数y=mx+4的表达式;
(2)试判断△AOB的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(11·湖州)(本小题10分)
如图,已知E、F分别是□ABCD的边BC、AD上的点,且BE=DF。
⑴求证:四边形AECF是平行四边形;
⑵若BC=10,∠BAC=90°,且四边形AECF是菱形,求BE的长。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com