
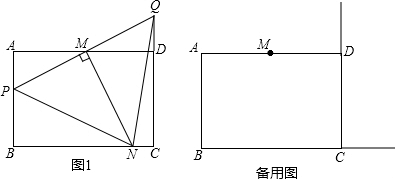
分析 (1)①由矩形的性质得出矩形∠B=90°,得出∠B+∠PMN=180°,证出点B、N、M、P四点共圆,即可得出点M在△PBN的外接圆上;
②作ME⊥BC于E,证明△AMP∽△EMN,由相似三角形的性质既可以求出PM与MN的关系,再由勾股定理表示出PN就可以求出结论;
(2)分两种情况,如图2,如图3,作BF⊥PN于F,CG⊥QN于G,作中线BS、CT,通过证明Rt△BFS≌Rt△CGT和△PBN≌△QCN,进一步由全等三角形的性质就可以得出结论.
解答 解:(1)①∵四边形ABCD是矩形,
∴∠B=90°,
∵MN⊥PQ,
∴∠PMN=90°,
∴∠B+∠PMN=180°,
∴点B、N、M、P四点共圆,
∴点M在△PBN的外接圆上;
②$\frac{PM}{PN}=\frac{3}{5}$是定值,理由:作ME⊥BC于E,如图1所示: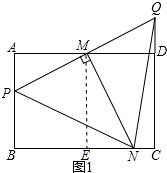
∴∠MEN=∠MEB=90°,∠AME=90°,
∴四边形ABEM是矩形,∠MEN=∠MAP,
∴AB=EM,
∵MN⊥PQ,
∴∠PMN=90°,
∴∠PMN=∠AME,
∴∠PMN-∠PME=∠AME-∠PME,
∴∠EMN=∠AMP,
∴△AMP∽△EMN,
∴$\frac{AM}{EM}=\frac{PM}{MN}$,
∴$\frac{AM}{AB}=\frac{PM}{MN}$,
∵AD=6,M是AD边的中点,
∴AM=$\frac{1}{2}$AD=3,
∵AB=4,
∴$\frac{PM}{MN}=\frac{3}{4}$.
在Rt△PMN中,设PM=3a,MN=4a,
由勾股定理得:PN=5a,
∴$\frac{PM}{PN}=\frac{3}{5}$;
(2)如图2,作BF⊥PN于F,CG⊥QN于G,作中线BS、CT,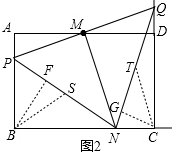
∴∠BFS=∠CGT=90°,BS=$\frac{1}{2}$PN,CT=$\frac{1}{2}$QN,
∵PN=QN,S△PBN=S△NCQ,
∴BF=CG,BS=CT,
在Rt△BFS和Rt△CGT中,
$\left\{\begin{array}{l}{BS=CT}\\{BF=CG}\end{array}\right.$,
∴Rt△BFS≌Rt△CGT(HL),
∴∠BSF=∠CTG,
∴∠BNP=$\frac{1}{2}$∠BSF=$\frac{1}{2}$∠CTG=∠CQN,
即∠BNP=∠CQN,
在△PBN和△QCN中
$\left\{\begin{array}{l}{∠BNP=∠CQN}\\{∠PBN=∠NCQ}\\{PN=QN}\end{array}\right.$,
∴△PBN≌△NCQ(AAS),
∴BN=CQ,
∴设AP=x.则BP=4-x,QC=4+x,则CN=6-(4+x)=2-x,
∵4-x≠2-x,
∴不合题意,舍去;
如图3,作BF⊥PN于F,CG⊥QN于G,作中线BS、CT,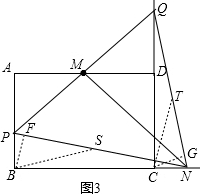
∴∠BFS=∠CGT=90°,BS=$\frac{1}{2}$PN,CT=$\frac{1}{2}$QN,
∵PN=QN,S△PBN=S△NCQ,
∴BF=CG,BS=CT,
在Rt△BFS和Rt△CGT中,
$\left\{\begin{array}{l}{BS=CT}\\{BF=CG}\end{array}\right.$,
∴Rt△BFS≌Rt△CGT(HL),
∴∠BSF=∠CTG,
∴∠BNP=$\frac{1}{2}$∠BSF=$\frac{1}{2}$∠CTG=∠CQN,
即∠BNP=∠CQN,
在△PBN和△QCN中
$\left\{\begin{array}{l}{∠BNP=∠CQN}\\{∠PBN=∠NCQ}\\{PN=QN}\end{array}\right.$,
∴△PBN≌△QCN(AAS),
∴PB=NC,BN=CQ,
∵AP=DQ,
∴AP+BP=AB=4①,AP+4=DQ+CD=BC+CN=6+BP,
∴AP-BP=2②,
∴①+②得:2AP=6
∴AP=3.
点评 本题考查了矩形的性质、全等三角形的判定及性质、勾股定理、相似三角形的判定及性质、四点共圆、三角形的面积公式的运用等知识;本题难度较大,综合性强,特别是(2)中,需要通过作辅助线多次证明三角形全等才能得出结果.


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:解答题
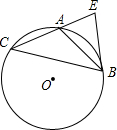 如图,△ABC内接于⊙O,过点B作⊙O的切线,交CA的延长线于点E,∠EBC=2∠C.
如图,△ABC内接于⊙O,过点B作⊙O的切线,交CA的延长线于点E,∠EBC=2∠C.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 品牌 | A | B | C | D | E | F | G |
| 百公里油耗(升) | 8.1 | 9.3 | 12.5 | 9 | 11 | 13 | 7.6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
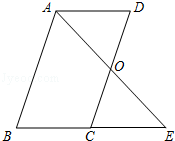 已知:如图,?ABCD中,O是CD的中点,连接AO并延长,交BC的延长线于点E.
已知:如图,?ABCD中,O是CD的中点,连接AO并延长,交BC的延长线于点E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com