
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У���C��B��E��y���ϣ�Rt��ABC�����仯�õ�Rt��EDO������B������Ϊ��0��1����OD��2�������ֱ仯�����ǣ� ��
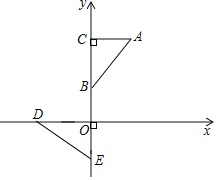
A.��ABC�Ƶ�C˳ʱ����ת90����������ƽ��5����λ����
B.��ABC�Ƶ�C��ʱ����ת90����������ƽ��5����λ����
C.��ABC�Ƶ�O˳ʱ����ת90����������ƽ��3����λ����
D.��ABC�Ƶ�O��ʱ����ת90����������ƽ��1����λ����

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��![]() ��x�ύ�ڵ�A��1��0������ y���ڵ�B��0��-2��.
��x�ύ�ڵ�A��1��0������ y���ڵ�B��0��-2��.
��1����ֱ��AB�ı���ʽ��
��2����C��ֱ��AB�ϵĵ㣬��CA=AB,������P(m��0)�Ҵ�ֱ��x���ֱ����ֱ��AB ���ڵ�D������D�����߶�BC�ϣ�д��m��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���ACB=90�㣬��B=30�㣬AC=2������ABC�ĸ�CD������CDB�ĸ�DC1������DC1B�ĸ�C1D1�������������ȥ����ô�õ���������Ӱ�����ε����֮��Ϊ__________.
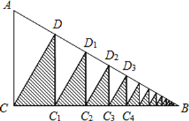
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У�E��AB�ߵ��е㣬��EC���۾���ABCD��ʹB�����ڵ�P�����ۺ�ΪEC������AP���ӳ�AP��CD��F�㣬
��1����֤���ı���AECFΪƽ���ı��Σ�
��2�����PA=PC������BP����֤����APB![]() ��EPC��
��EPC��
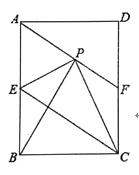
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2019���й����������ղ���������2019��4��29���ڱ�������������չ�������˴����οͲι���������һС�����ڼ�ƽ��ÿ����������Լ��8���ˣ��Ѽѵ�5��ͬѧ��ɵ�ѧϰС�飬�����������һ���������ι۵IJ����οͣ�������������ڲι�����ʱ�䣬�������ݽ��������������ͷ�������������˲�����Ϣ��
a���ι�ʱ���Ƶ���ֲ������£�
ʱ�� | Ƶ���������� | Ƶ�� |
| 25 | 0.050 |
| 85 |
|
| 160 | 0.320 |
| 139 | 0.278 |
|
| 0.100 |
| 41 | 0.082 |
�ϼ� |
| 1.000 |
b���ι�ʱ���Ƶ���ֲ�ֱ��ͼ��ͼ��
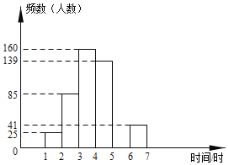
��������ͼ���ṩ����Ϣ������������⣺
��1��������õĵ��鷽ʽ���� ����
��2������![]() �� ����
�� ����![]() �� ����
�� ����![]() �� ����
�� ����
��3�����벹ȫƵ���ֲ�ֱ��ͼ��
��4�����������һ������ƽ��ÿ��ι�ʱ��С��4Сʱ���ο�Լ�ж������ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����û����������Բ�������£����ÿ̶ȳߺ�һ�����ǰ廭����һ���ǵ�ƽ���ߣ����������������ģ���ͼ:
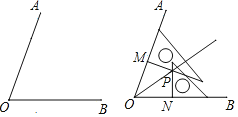
��1�����ÿ̶ȳ��ڡ�AOB������OA��OB�Ϸֱ�ȡOM��ON��
��2�������������ǰ壬�ֱ����M��N��OM��ON�Ĵ��ߣ�����ΪP��
��3��������OP��
������OPΪ��AOB��ƽ���ߣ���д��С�ֵĻ���������______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У���������![]() ��m��0������ƽ��
��m��0������ƽ��![]() ����λ���Ⱥ�õ�������G2����A��������G2�Ķ��㣮
����λ���Ⱥ�õ�������G2����A��������G2�Ķ��㣮
��1��ֱ��д����A�����ꣻ
��2�����㣨0��![]() ����ƽ����x���ֱ��l��������G2����B��C���㣮
����ƽ����x���ֱ��l��������G2����B��C���㣮
�ٵ���BAC��90��ʱ����������G2�ı���ʽ��
����60������BAC��120����ֱ��д��m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x��һԪ���η���x2+2��m��1��x+m2��3��0����������ȵ�ʵ������
��1����m��ȡֵ��Χ��
��2����mΪ�Ǹ��������Ҹ÷��̵ĸ���������������m��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
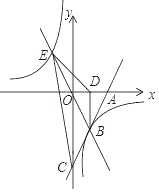
����Ŀ����ͼ��һ�κ�����ͼ����x�ᡢy��ֱ���A��C���㣬�뷴����������ͼ����B�㣬B���ڵ������ޣ�BD��ֱƽ��OA������ΪD��OB��![]() ��OA��BD��
��OA��BD��
��1�����һ�κ����ͷ����������Ľ���ʽ��
��2���ӳ�BO��������������ͼ���ڵ�E������ED��EC�����ı���BCED�������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com