练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】小林在没有量角器和圆规的情况下，利用刻度尺和一副三角板画出了一个角的平分线，他的作法是这样的：如图:

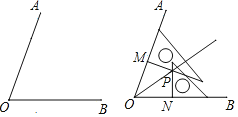
    （1）利用刻度尺在∠AOB的两边OA，OB上分别取OM＝ON；

    （2）利用两个三角板，分别过点M，N画OM，ON的垂线，交点为P；

    （3）画射线OP．

    则射线OP为∠AOB的平分线．请写出小林的画法的依据______．

    【答案】斜边和一条直角边分别相等的两个直角三角形全等；全等三角形的对应角相等；两点确定一条直线

    【解析】

    利用“HL”判断Rt△OPM≌Rt△OPN，从而得到∠POM=∠PON．

    有画法得OM＝ON，∠OMP＝∠ONP＝90°，则可判定Rt△OPM≌Rt△OPN，

    所以∠POM＝∠PON，

    即射线OP为∠AOB的平分线．

    故答案为斜边和一条直角边分别相等的两个直角三角形全等；全等三角形的对应角相等；两点确定一条直线．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

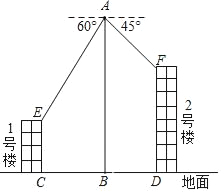
    【题目】如图，某兴趣小组用无人机进行航拍测高，无人机从1号楼和2号楼的地面正中间B点垂直起飞到高度为50米的A处，测得1号楼顶部E的俯角为60°，测得2号楼顶部F的俯角为45°．已知1号楼的高度为20米，则2号楼的高度为_____米(结果保留根号)．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在Rt△ABC中，∠BAC=90°，BC=10，tan∠ABC=，点O是AB边上动点，以O为圆心，OB为半径的⊙O与边BC的另一交点为D，过点D作AB的垂线，交⊙O于点E，联结BE、AE

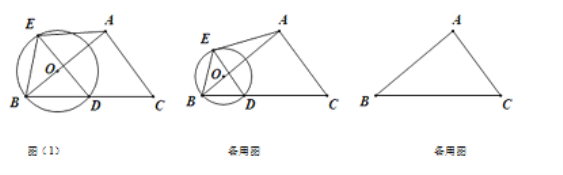
    （1）如图（1），当AE∥BC时，求⊙O的半径长；

    （2）设BO=x，AE=y，求y关于x的函数关系式，并写出定义域；

    （3）若以A为圆心的⊙A与⊙O有公共点D、E，当⊙A恰好也过点C时，求DE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下面是小明设计的“在一个平行四边形内作菱形”的尺规作图过程．

    已知：四边形是平行四边形．

    求作：菱形（点在上，点在上）．

    作法：①以为圆心，长为半径作弧，交于点；

    ②以为圆心，长为半径作弧，交于点；

    ③连接．所以四边形为所求作的菱形．

    根据小明设计的尺规作图过程，

    （1）使用直尺和圆规，补全图形；（保留作图痕迹）

    （2）完成下面的证明．

    证明：∵，，

    ∴　 　＝　 　．

    在中，．

    即．

    ∴四边形为平行四边形．

    ∵，

    ∴四边形为菱形（　 　）（填推理的依据）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系xOy中，点C，B，E在y轴上，Rt△ABC经过变化得到Rt△EDO，若点B的坐标为（0，1），OD＝2，则这种变化可以是（ ）

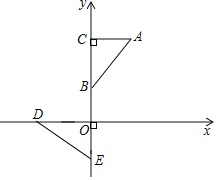
    A.△ABC绕点C顺时针旋转90°，再向下平移5个单位长度

    B.△ABC绕点C逆时针旋转90°，再向下平移5个单位长度

    C.△ABC绕点O顺时针旋转90°，再向左平移3个单位长度

    D.△ABC绕点O逆时针旋转90°，再向右平移1个单位长度

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校诗词知识竞赛培训活动中，在相同条件下对甲、乙两名学生进行了10次测验，他们的10次成绩如下（单位：分）：整理、分析过程如下，请补充完整．

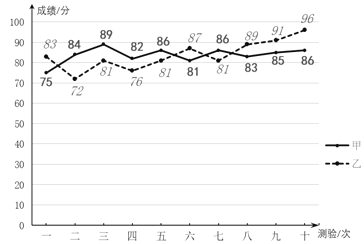
    （1）按如下分数段整理、描述这两组数据：

    成绩x

    学生

    70≤x≤74

    75≤x≤79

    80≤x≤84

    85≤x≤89

    90≤x≤94

    95≤x≤100

    甲

    ______

    ______

    ______

    ______

    ______

    ______

    乙

    1

    1

    4

    2

    1

    1

    （2）两组数据的极差、平均数、中位数、众数、方差如下表所示：

    学生

    极差

    平均数

    中位数

    众数

    方差

    甲

    ______

    83.7

    ______

    86

    13.21

    乙

    24

    83.7

    82

    ______

    46.21

    （3）若从甲、乙两人中选择一人参加知识竞赛，你会选______（填“甲”或“乙），理由为______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

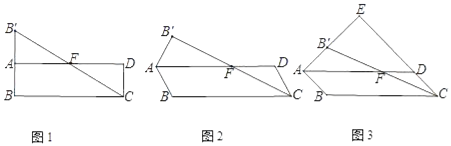
    【题目】在ABCD中，点B关于AD的对称点为B′，连接AB′，CB′，CB′交AD于F点．

    （1）如图1，∠ABC=90°，求证：F为CB′的中点；

    （2）小宇通过观察、实验、提出猜想：如图2，在点B绕点A旋转的过程中，点F始终为CB′的中点．小宇把这个猜想与同学们进行交流，通过讨论，形成了证明该猜想的几种想法：

    想法1：过点B′作B′G∥CD交AD于G点，只需证三角形全等；

    想法2：连接BB′交AD于H点，只需证H为BB′的中点；

    想法3：连接BB′，BF，只需证∠B′BC=90°．

    …

    请你参考上面的想法，证明F为CB′的中点．（一种方法即可）

    （3）如图3，当∠ABC=135°时，AB′，CD的延长线相交于点E，求的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

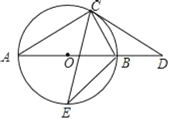
    【题目】AB为⊙O直径，C为⊙O上的一点，过点C的切线与AB的延长线相交于点D，CA＝CD．

    （1）连接BC，求证：BC＝OB；

    （2）E是中点，连接CE，BE，若BE＝2，求CE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

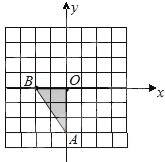
    【题目】如图，在平面直角坐标系中，已知△AOB，A（0，﹣3），B（﹣2，0）．将△OAB先绕点B 逆时针旋转90°得到△BO1A1，再把所得三角形向上平移2个单位得到△B1A2O2；

    （1）在图中画出上述变换的图形，并涂黑；

    （2）求△OAB在上述变换过程所扫过的面积．

    查看答案和解析>>

    同步练习册答案