
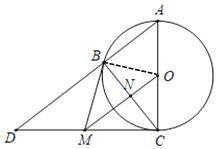
【题目】如图,⊙O是△ABC的外接圆,AC为直径,过C点作⊙O的切线,与AB延长线交于点D,M为CD的中点,连接BM,OM,且BC与OM相交于点N.
(1)求证:BM与⊙O相切;
(2)求证:2DM2=BDOM;
(3)若sinA=![]() ,BM=3,求AB的长.
,BM=3,求AB的长.

【答案】(1)见解析;(2)见解析;(3)5
【解析】
(1)连接OB,知∠OCB=∠OBC,由直角三角形性质知BM=CM=DM,得∠MBC=∠MCB,依据CD是⊙O的切线知∠OCB+∠DCB=90°,据此可得∠OBC+∠MBC=90°,可得结论;
(2)先证△DBC∽△DCA得![]() ,即CD2=BDDA,再证OM是△ACD的中位线得AD=2OE,两者结合即可得;
,即CD2=BDDA,再证OM是△ACD的中位线得AD=2OE,两者结合即可得;
(3)由直角三角形的性质可得CD=2BM=6,即可求AD=9,代入CD2=ADBD,可求BD的长,即可求AB的长.
证明:(1)连接OB
∵OB=OC
∴∠OBC=∠OCB
∵AC是直径
∴∠ABC=∠DBC=90°
∵点M是CD中点,
∴BM=CM=DM
∴∠MBC=∠MCB
∵CD是⊙O切线
∴∠ACD=90°
∴∠OCB+∠MCB=90°
∴∠OBC+∠MBC=90°
即OB⊥BM,且OB是半径
∴BM是⊙O的切线
(2)∵AO=CO,DM=CM
∴AD=2OM,AD∥OM
∵∠ACB+∠DCB=90°,∠A+∠ACB=90°
∴∠A=∠DCB,且∠D=∠D
∴△ACD∽△CBD
∴![]()
∴CD2=ADBD
∴(2DM)2=2OMBD
∴2DM=BDOM
(3)∵∠DBC=90°,点M是CD的中点
∴CD=2BM=6
∵sinA=![]() =
=![]() ,
,
∴AD=9
∵CD2=ADBD
∴BD=4
∴AB=AD﹣BD=5


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系内,以原点O为圆心,1为半径作圆,点P在直线![]() 上运动,过点P作该圆的一条切线,切点为A,则PA的最小值为
上运动,过点P作该圆的一条切线,切点为A,则PA的最小值为![]()
![]()
A. 3 B. 2 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了扎实推进精准扶贫工作,某地出台了民生兜底、医保脱贫、教育救助、产业扶持、养老托管和易地搬迁这六种帮扶措施,每户贫困户都享受了2到5种帮扶措施,现把享受了2种、3种、4种和5种帮扶措施的贫困户分别称为A、B、C、D类贫困户.为检査帮扶措施是否落实,随机抽取了若干贫困户进行调查,现将收集的数据绘制成下面两幅不完整的统计图:
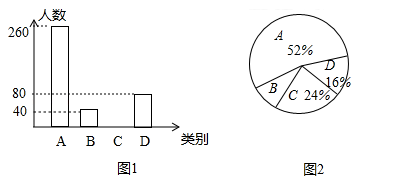
请根据图中信息回答下面的问题:
(1)本次抽样调查了多少户贫困户?
(2)抽查了多少户C类贫困户?并补全统计图;
(3)若该地共有13000户贫困户,请估计至少得到4项帮扶措施的大约有多少户?
(4)为更好地做好精准扶贫工作,现准备从D类贫困户中的甲、乙、丙、丁四户中随机选取两户进行重点帮扶,请用树状图或列表法求出恰好选中甲和丁的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】萧山区垃圾分类掀起“绿色革命”为调查居民对垃圾分类的了解情况,调查小组对某小区进行抽样调查并将调查结果绘制成了统计图(如图).已知调查中“基本了解”的人数占调查人数的60%.
(1)计算此次调查人数,并补全统计图;
(2)若该小区有住户1000人,请估计该小区对垃圾分类“基本了解”的人数.
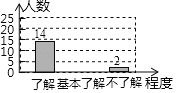
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AB<BC.
(1)利用尺规作图,在AD边上确定点E,使点E到边AB,BC的距离相等(不写作法,保留作图痕迹);
(2)若BC=8,CD=5,则DE= .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=3,CB=2,点E为线段AB上的动点,将△CBE沿CE折叠,使点B落在矩形内点F处,下列结论正确的是_____(写出所有正确结论的序号)
①当E为线段AB中点时,AF∥CE;
②当E为线段AB中点时,AF=![]() ;
;
③当A、F、C三点共线时,AE=![]() ;
;
④当A、F、C三点共线时,△CEF≌△AEF.
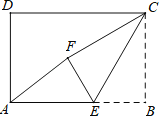
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某射击运动员练习射击,5次成绩分别是:8、9、7、8、x(单位:环).下列说法中正确的是( )
A. 若这5次成绩的中位数为8,则x=8
B. 若这5次成绩的众数是8,则x=8
C. 若这5次成绩的方差为8,则x=8
D. 若这5次成绩的平均成绩是8,则x=8
查看答案和解析>>
科目:初中数学 来源: 题型:
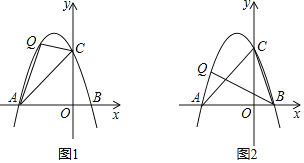
【题目】在平面直角坐标系中,点O(0,0),点A(﹣3,0).已知抛物线y=﹣x2+2mx+3(m为常数),顶点为P.
(1)当抛物线经过点A时,顶点P的坐标为 ;
(2)在(1)的条件下,此抛物线与x轴的另一个交点为点B,与y轴交于点C.点Q为直线AC上方抛物线上一动点.
①如图1,连接QA、QC,求△QAC的面积最大值;
②如图2,若∠CBQ=45°,请求出此时点Q坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
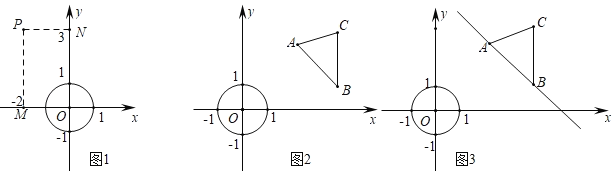
【题目】在平面直角坐标系xOy,对于点P(xp,yp)和图形G,设Q(xQ,yQ)是图形G上任意一点,|xp﹣xQ|的最小值叫点P和图形G的“水平距离”,|yp﹣yQ|的最小值叫点P和图形G的“竖直距离”,点P和图形G的“水平距离”与“竖直距离”的最大值叫做点P和图形G的“绝对距离”
例如:点P(﹣2,3)和半径为1的⊙O,因为⊙O上任一点Q(xQ,yQ)满足﹣1≤xQ≤1,﹣1≤yQ≤1,点P和⊙O的“水平距离”为|﹣2﹣xQ|的最小值,即|﹣2﹣(﹣1)|=1,点P和⊙O的“竖直距离”为|3﹣yQ|的最小值即|3﹣1|=2,因为2>1,所以点P和⊙O的“绝对距离”为2.
已知⊙O半径为1,A(2,![]() ),B(4,1),C(4,3)
),B(4,1),C(4,3)
(1)①直接写出点A和⊙O的“绝对距离”
②已知D是△ABC边上一个动点,当点D与⊙O的“绝对距离”为2时,写出一个满足条件的点D的坐标;
(2)已知E是△ABC边一个动点,直接写出点E与⊙O的“绝对距离”的最小值及相应的点E的坐标
(3)已知P是⊙O上一个动点,△ABC沿直线AB平移过程中,直接写出点P与△ABC的“绝对距离”的最小值及相应的点P和点C的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com