
【题目】商场正在销售帐篷和棉被两种防寒商品,已知购买 ![]() 顶帐篷和
顶帐篷和 ![]() 床棉被共需
床棉被共需 ![]() 元,购买
元,购买 ![]() 顶帐篷和
顶帐篷和 ![]() 床棉被共需
床棉被共需 ![]() 元.
元.
(1)求 ![]() 顶帐篷和
顶帐篷和 ![]() 床棉被的价格各是多少元?
床棉被的价格各是多少元?
(2)某学校准备购买这两种防寒商品共 ![]() 件,送给青海玉树灾区,要求每种商品都要购买,且帐篷的数量多于棉被的数量,但因为学校资金不足,购买总金额不能超过
件,送给青海玉树灾区,要求每种商品都要购买,且帐篷的数量多于棉被的数量,但因为学校资金不足,购买总金额不能超过 ![]() 元,请问学校共有几种购买方案?(要求写出具体的购买方案)
元,请问学校共有几种购买方案?(要求写出具体的购买方案)
【答案】(1)110元,80元;(2)共有三种方案:①购买41顶帐篷39床被子,②购买42顶帐篷38床被子,③购买43顶帐篷37床被子
【解析】
(1)根据1顶帐篷的钱数+2床棉被的钱数=270元,2顶帐篷的钱数+3床棉被的钱数=460元,可得出方程组,解出即可;
(2)设帐篷a顶,则棉被(80-a)床,再由购买总金额不能超过7700元,可得出不等式组,解出a的取值,再根据a为正整数,列出方案即可.
解:(1)设一顶帐篷x元,一床棉被y元,
则![]() ,
,
解得:![]() ,
,
答:1顶帐篷的价格为110元,![]() 床棉被的价格是80元;
床棉被的价格是80元;
(2)设帐篷a顶,则棉被(80-a)床,
则![]() ,
,
解得:![]() ,
,
∴a取41,42,43共三种,
共有三种方案:
①购买41顶帐篷39床被子;
②购买42顶帐篷38床被子;
③购买43顶帐篷37床被子.


 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:初中数学 来源: 题型:
【题目】“十一”黄金周,坚胜家电城大力促销,收银情况一直看好![]() 下表为当天与前一天的营业额的涨跌情况
下表为当天与前一天的营业额的涨跌情况![]() 已知9月30日的营业额为26万元.
已知9月30日的营业额为26万元.
10月1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 |
4 | 3 | 2 | 0 |
|
|
|
![]() 黄金周内收入最低的哪一天?
黄金周内收入最低的哪一天?![]() 直接回答,不必写过程
直接回答,不必写过程![]() .
.
![]() 黄金周内平均每天的营业额是多少?
黄金周内平均每天的营业额是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料: 小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如:![]() ,善于思考的小明进行了以下探索:
,善于思考的小明进行了以下探索:
设![]() (其中
(其中![]() 均为整数),则有
均为整数),则有![]() .
.
∴![]() .这样小明就找到了一种把部分
.这样小明就找到了一种把部分![]() 的式子化为平方式的方法.
的式子化为平方式的方法.
请你仿照小明的方法探索并解决下列问题:
当![]() 均为正整数时,若
均为正整数时,若![]() ,用含m、n的式子分别表示
,用含m、n的式子分别表示![]() ,得
,得![]() = ,
= ,![]() = ;
= ;
(2)利用所探索的结论,找一组正整数![]() ,填空: + =( +
,填空: + =( + ![]() )2;
)2;
(3)若![]() ,且
,且![]() 均为正整数,求
均为正整数,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】鲁能巴蜀中学2018年校艺术节“巴蜀好声音”独唱预选赛中,初二年级25名同学的成绩![]() 满分为10分
满分为10分![]() 统计如下:
统计如下:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,10
,10
![]() 分及以上为A级,
分及以上为A级,![]() 分为B级
分为B级![]() 包括
包括![]() 分和
分和![]() 分
分![]() ,
,![]() 分为C级
分为C级![]() 包括
包括![]() 分和
分和![]() 分
分![]() ,
,![]() 分以下为D级
分以下为D级![]() 请把下面表格补充完整;
请把下面表格补充完整;
等级 | A | B | C | D |
人数 | 4 | 8 |
![]() 级8位同学成绩的中位数是多少,众数是多少;
级8位同学成绩的中位数是多少,众数是多少;
![]() 若成绩为A级的同学将参加学校的汇演,请求出初二年级A级同学的平均成绩?
若成绩为A级的同学将参加学校的汇演,请求出初二年级A级同学的平均成绩?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c的图象如图所示,则一次函数y=bx+b2﹣4ac与反比例函数y= ![]() 在同一坐标系内的图象大致为( )
在同一坐标系内的图象大致为( ) 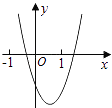
A.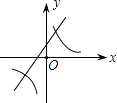
B.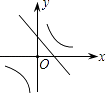
C.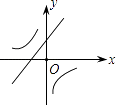
D.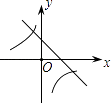
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:对于二次三项式 ![]() ,能直接用公式法进行因式分解,得到
,能直接用公式法进行因式分解,得到 ![]() ,但对于二次三项式
,但对于二次三项式 ![]() ,就不能直接用公式法了.我们可以采用这样的方法:在二次三项式
,就不能直接用公式法了.我们可以采用这样的方法:在二次三项式 ![]() 中先加上一项
中先加上一项 ![]() ,使其成为完全平方式,再减去
,使其成为完全平方式,再减去 ![]() 这项,使整个式子的值不变,于是:
这项,使整个式子的值不变,于是:

像这样把二次三项式分解因式的方法叫做添(拆)项法.
![]() 问题解决:请用上述方法将二次三项式
问题解决:请用上述方法将二次三项式 ![]() 分解因式.
分解因式.
(2)拓展应用:二次三项式 ![]() 有最小值或有最大值吗?如果有,请你求出来并说明理由.
有最小值或有最大值吗?如果有,请你求出来并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数 ![]() ,则下列结论不正确的是( )
,则下列结论不正确的是( )
A.图象必经过点(-1,5)
B.图象的两个分支分布在第二、四象限
C.y随x的增大而增大
D.若x>1,则-5<y<0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,有理数包括整数、有限小数和无限循环小数,事实上,所有的有理数都可以化为分数形式(整数可看作分母为1的分数),那么无限循环小数如何表示为分数形式呢?请看以下示例:
例:将![]() 化为分数形式,
化为分数形式,
由于![]() ,设
,设![]() ,①
,①
得![]() ,②
,②
②①得![]() ,解得
,解得![]() ,于是得
,于是得![]() .
.
同理可得![]() ,
,![]() .
.
根据以上阅读,回答下列问题:(以下计算结果均用最简分数表示)
(类比应用)
(1)![]() ;
;
(2)将![]() 化为分数形式,写出推导过程;
化为分数形式,写出推导过程;
(迁移提升)
(3)![]() ,
,![]() ;(注
;(注![]() ,
,![]() )
)
(拓展发现)
(4)若已知![]() ,则
,则![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com