
如图1,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于F.
(1)证明:PC=PE;
(2)求∠CPE的度数;
(3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°时,连接CE,试探究线段AP与线段CE的数量关系,并说明理由.
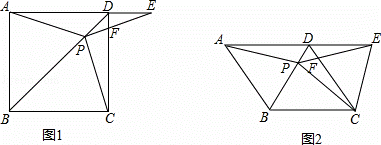
(1)证明:在正方形ABCD中,AB=BC,
∠ABP=∠CBP=45°,
在△ABP和△CBP中,
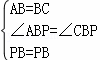 ,
,
∴△ABP≌△CBP(SAS),
∴PA=PC,
∵PA=PE,
∴PC=PE;
(2)由(1)知,△ABP≌△CBP,
∴∠BAP=∠BCP,
∴∠DAP=∠DCP,
∵PA=PC,
∴∠DAP=∠E,
∴∠DCP=∠E,
∵∠CFP=∠EFD(对顶角相等),
∴180°﹣∠PFC﹣∠PCF=180°﹣∠DFE﹣∠E,
即∠CPF=∠EDF=90°;
(3)在正方形ABCD中,AB=BC,∠ABP=∠CBP=45°,
在△ABP和△CBP中,
∴△ABP≌△CBP(SAS),
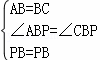
∴PA=PC,∠BAP=∠BCP,
∵PA=PE,
∴PC=PE,
∴∠DAP=∠DCP,
∵PA=PC,
∴∠DAP=∠E,
∴∠DCP=∠E
∵∠CFP=∠EFD(对顶角相等),
∴180°﹣∠PFC﹣∠PCF=180°﹣∠DFE﹣∠E,
即∠CPF=∠EDF=180°﹣∠ADC=180°﹣120°=60°,
∴△EPC是等边三角形,
∴PC=CE,
∴AP=CE;



 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
把所有正奇数从小到大排列,并按如下规律分组:(1),(3,5,7),(9,11,13,15,17),(19,21,23,25,27,29,31),…,现有等式Am=(i,j)表示正奇数m是第i组第j个数(从左往右数),如A7=(2,3),则A2015=( )
A. (31,50) B. (32,47) C. (33,46) D. (34,42)
查看答案和解析>>
科目:初中数学 来源: 题型:
阅读理解
抛物线y=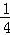 x2上任意一点到点(0,1)的距离与到直线y=﹣1的距离相等,你可以利用这一性质解决问题.
x2上任意一点到点(0,1)的距离与到直线y=﹣1的距离相等,你可以利用这一性质解决问题.
问题解决
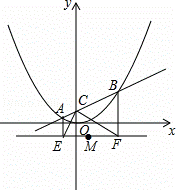
如图,在平面直角坐标系中,直线y=kx+1与y轴交于C点,与函数y=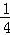 x2的图象交于A,B两点,分别过A,B两点作直线y=﹣1的垂线,交于E,F两点.
x2的图象交于A,B两点,分别过A,B两点作直线y=﹣1的垂线,交于E,F两点.
(1)写出点C的坐标,并说明∠ECF=90°;
(2)在△PEF中,M为EF中点,P为动点.
①求证:PE2+PF2=2(PM2+EM2);
②已知PE=PF=3,以EF为一条对角线作平行四边形CEDF,若1<PD<2,试求CP的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
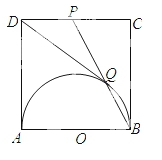
如图,正方形ABCD边长为1,以AB为直径作半圆,点P是CD 中点,BP与半圆交于点Q,连结DQ.给出如下结论:①DQ=1;②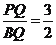 ;③S△PDQ=
;③S△PDQ=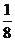 ;④cos∠ADQ=
;④cos∠ADQ=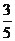 .其中正确结论是_________.(填写序号)
.其中正确结论是_________.(填写序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com