
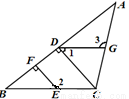
(本题满分10分) 如图,在△ABC中,点E、G分别在BC、AC上,CD⊥AB,EF⊥AB,垂足分别为D、F.已知∠1+∠2=180°,∠3=105°,求∠ACB的度数.请将求∠ACB度数的过程填写完整.
【解析】
∵EF⊥AB,CD⊥AB,(已知)
∴∠BFE=90°,∠BDC=90°,
理由是: .
∴∠BFE=∠BDC,
∴EF∥CD,理由是: .
∴ ∠2+∠ =180°,理由是: .
又∵ ∠1 +∠2=180°(已知),
∴ ∠1 = .
∴ BC∥ ,理由是: .
∴∠3 = ,理由是: .
又∵∠3 = 105°(已知),
∴∠ACB= .
(垂直的定义),(同位角相等,两直线平行),∠BCD,(两直线平行,同旁内角互补),∠BCD,DG,(内错角相等,两直线平行),∠ACB,(两直线平行,同位角相等),105°
【解析】
试题分析:根据垂直的定义可得∠BFE=∠BDC=90°,然后根据同位角相等,两直线平行可得CD∥EF,再根据两直线平行,同位角相等可得∠2=∠BCD,然后求出∠1=∠BCD,再根据内错角相等,两直线平行,然后根据两直线平行,同位角相等可得∠3=∠ACB.
试题解析:∵EF⊥AB,CD⊥AB,(已知)
∴∠BFE=90°,∠BDC=90°,(垂直的定义).
∴∠BFE=∠BDC,
∴EF∥CD,(同位角相等,两直线平行).
∴ ∠2+∠BCD=180°,(两直线平行,同旁内角互补).
又∵ ∠1 +∠2=180°(已知),
∴ ∠1 = ∠BCD.
∴ BC∥ DG,(内错角相等,两直线平行).
∴∠3 = ∠ACB ,(两直线平行,同位角相等).
又∵∠3 = 105°(已知)
∴∠ACB= 105°
考点:平行线的性质和判定.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2014-2015学年江苏省兴化顾庄等三校九年级上学期期末考试数学试卷(解析版) 题型:填空题
一个不透明的袋中装有2枚白色棋子和n枚黑色棋子,它们除颜色不同外,其余均相同.若小明从中随机摸出一枚棋子,多次实验后发现摸到黑色棋子的频率稳定在80%.则n很可能是 枚.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年重庆开县八年级上学期期末考试数学试卷(解析版) 题型:解答题
如图,已知:在平面直角坐标系中,每个小正方形的边长为1, 的顶点都在格点上,点A的坐标为(-3,2)。请按要求分别完成下列各小题:
的顶点都在格点上,点A的坐标为(-3,2)。请按要求分别完成下列各小题:
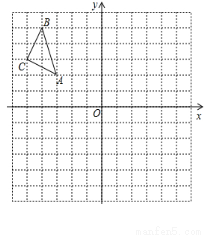
(1)把△ABC向下平移4个单位,得到△A1B1C1,画出△A1B1C1,点A1的坐标为
(2)画出△ABC关于y轴对称的△A2B2C2;点C2的坐标是
(3)求△ABC的面积。
查看答案和解析>>
科目:初中数学 来源:2014-2015学年重庆开县八年级上学期期末考试数学试卷(解析版) 题型:选择题
如图,CD,CE,CF分别是△ABC的高、角平分线、中线,则下列各式中错误的是( )
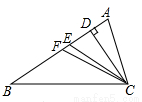
A.AB=2BF B.AE=BE C.∠ACE=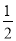 ∠ACB D.CD⊥BE
∠ACB D.CD⊥BE
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省兴化顾庄等三校七年级上学期期末考试数学试卷(解析版) 题型:解答题
(本题满分12分)如图,已知∠AOB内部有三条射线,OE平分∠BOC,OF平分∠AOC.
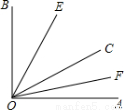
(1)若∠AOB=90°,∠AOC=30°,求∠EOF的度数;
(2)若∠AOB=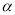 ,求∠EOF的度数(写出求解过程);
,求∠EOF的度数(写出求解过程);
(3)若将条件中“OE平分∠BOC,OF平分∠AOC.平分”改为“∠EOB=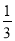 ∠COB,∠COF=
∠COB,∠COF=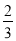 ∠COA”,且∠AOB=
∠COA”,且∠AOB=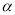 ,求∠EOF的度数(写出求解过程).
,求∠EOF的度数(写出求解过程).
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省兴化顾庄等三校七年级上学期期末考试数学试卷(解析版) 题型:计算题
(本题满分12分)计算:
(1)-4+28-(-19)+(-24); (2)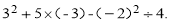
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省兴化顾庄等三校八年级上学期期末考试数学试卷(解析版) 题型:解答题
(本题满分10分)已知四边形ABCD是矩形,对角线AC和BD相交于点P,若在矩形的上方加一个△DEA,且使DE∥AC,AE∥BD.

(1)求证:四边形DEAP是菱形;
(2)若AE=CD,求∠DPC的度数.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省江阴市八年级上学期期末调研考试数学试卷(解析版) 题型:填空题
如图,在△ABC中,AB=AC=5,BC=6,点E、F是中线AD上的两点,则图中阴影部分的面积是
.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com