
(本题满分12分)如图,已知∠AOB内部有三条射线,OE平分∠BOC,OF平分∠AOC.
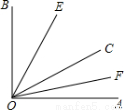
(1)若∠AOB=90°,∠AOC=30°,求∠EOF的度数;
(2)若∠AOB=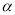 ,求∠EOF的度数(写出求解过程);
,求∠EOF的度数(写出求解过程);
(3)若将条件中“OE平分∠BOC,OF平分∠AOC.平分”改为“∠EOB=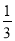 ∠COB,∠COF=
∠COB,∠COF=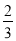 ∠COA”,且∠AOB=
∠COA”,且∠AOB=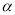 ,求∠EOF的度数(写出求解过程).
,求∠EOF的度数(写出求解过程).
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:2014-2015学年江苏省兴化顾庄等三校九年级上学期期末考试数学试卷(解析版) 题型:填空题
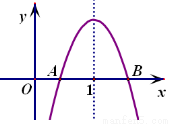
如图,抛物线的对称轴是直线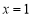 ,与x轴交于A、B两点,若B点坐标是
,与x轴交于A、B两点,若B点坐标是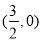 ,则A点的坐标是 .
,则A点的坐标是 .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年重庆开县八年级上学期期末考试数学试卷(解析版) 题型:选择题
如图,△ABC中,AB=AC,∠A=36°,AB的垂直平分线DE交AC于D,交AB于E,则∠BDC的度数为( )
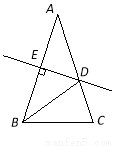
A. 72° B. 36° C. 60° D. 82°
查看答案和解析>>
科目:初中数学 来源: 题型:
如图1,正方形ABCD的边AB、AD分别在等腰直角△AEF的腰AE、AF上,点C在△AEF内,则有DF=BE(不必证明).将正方形ABCD绕点A逆时针旋转一定角度α(0°<α<90°)后,连接BE、DF.请在图2中用实线补全图形,这时DF=BE还成立吗?请说明理由.
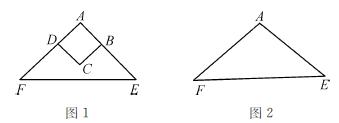
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省兴化顾庄等三校七年级上学期期末考试数学试卷(解析版) 题型:解答题
(本题满分10分) 如图,在△ABC中,点E、G分别在BC、AC上,CD⊥AB,EF⊥AB,垂足分别为D、F.已知∠1+∠2=180°,∠3=105°,求∠ACB的度数.请将求∠ACB度数的过程填写完整.
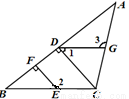
【解析】
∵EF⊥AB,CD⊥AB,(已知)
∴∠BFE=90°,∠BDC=90°,
理由是: .
∴∠BFE=∠BDC,
∴EF∥CD,理由是: .
∴ ∠2+∠ =180°,理由是: .
又∵ ∠1 +∠2=180°(已知),
∴ ∠1 = .
∴ BC∥ ,理由是: .
∴∠3 = ,理由是: .
又∵∠3 = 105°(已知),
∴∠ACB= .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省兴化顾庄等三校七年级上学期期末考试数学试卷(解析版) 题型:填空题
如图,B处在A处的南偏西45°方向,C处在A处的南偏东15°方向,C处在B处的北偏东85°方向,则∠ACB的度数为 .
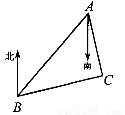
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省江阴市八年级上学期期末调研考试数学试卷(解析版) 题型:填空题
如图,在△ABC中,AB=BC,∠ABC=90°,E是AB上一点,BE=2,AE=3BE,P是AC上一动点,则PB+PE的最小值是 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com