
(本题满分10分)已知四边形ABCD是矩形,对角线AC和BD相交于点P,若在矩形的上方加一个△DEA,且使DE∥AC,AE∥BD.

(1)求证:四边形DEAP是菱形;
(2)若AE=CD,求∠DPC的度数.
科目:初中数学 来源: 题型:
如图,在△ABC中,点D,E分别在边AC,AB上,BD与CE交于点O,给出下列三个条件:①∠EBO=∠DCO;②BE=CD;③OB=OC.
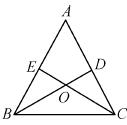
(1)上述三个条件中,由哪两个条件可以判定△ABC是等腰三角形?(用序号写出所有成立的情形)
(2)请选择(1)中的一种情形,写出证明过程.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省兴化顾庄等三校七年级上学期期末考试数学试卷(解析版) 题型:解答题
(本题满分10分) 如图,在△ABC中,点E、G分别在BC、AC上,CD⊥AB,EF⊥AB,垂足分别为D、F.已知∠1+∠2=180°,∠3=105°,求∠ACB的度数.请将求∠ACB度数的过程填写完整.
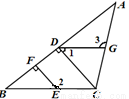
【解析】
∵EF⊥AB,CD⊥AB,(已知)
∴∠BFE=90°,∠BDC=90°,
理由是: .
∴∠BFE=∠BDC,
∴EF∥CD,理由是: .
∴ ∠2+∠ =180°,理由是: .
又∵ ∠1 +∠2=180°(已知),
∴ ∠1 = .
∴ BC∥ ,理由是: .
∴∠3 = ,理由是: .
又∵∠3 = 105°(已知),
∴∠ACB= .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省兴化顾庄等三校八年级上学期期末考试数学试卷(解析版) 题型:填空题
在边长为16cm的正方形铁皮上剪去一个圆,则剩下的铁皮的面积S(cm2)与圆的半径r(cm)之间的函数表达式为 (不要求写自变量的取值范围).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com