
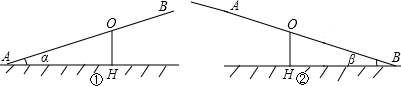
分析 根据三角函数的知识分别用OH表示出AO,BO的长,再根据不等臂跷跷板AB长4米,即可列出方程求解即可.
解答 解:根据题意得:AO=OH÷sinα,BO=OH÷sinβ,
AO+BO=OH÷sinα+OH÷sinβ,
即OH÷sinα+OH÷sinβ=4,
则OH=$\frac{4sinα•sinβ}{sinα+sinβ}$=$\frac{4×sin30°×sin37°}{sin30°+sin37°}$=$\frac{4×\frac{1}{2}×0.6}{\frac{1}{2}+0.6}$=$\frac{12}{11}$(米).
即故跷跷板AB的支撑点O到地面的高度OH是$\frac{12}{11}$米.
点评 本题考查的是解直角三角形的应用,根据题意利用锐角三角函数的定义得出求OH的关系式是解答此题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a+b+c | B. | -a+3b-c | C. | a+b-c | D. | 2b-2c |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a<-2 | B. | a=-2 | C. | a>-2 | D. | a≥-2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com