
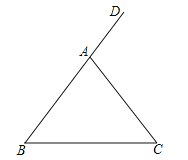
【题目】如图,在△ABC中,AB=AC,∠DAC是△ABC的一个外角.
实验与操作:
根据要求进行尺规作图,并在图中标明相应字母(保留作图痕迹,不写作法)
(1)作∠DAC的平分线AM;
(2)作线段AC的垂直平分线,与AM交于点F,与BC边交于点E,连接AE,CF.
猜想并判断四边形AECF的形状并加以证明.
【答案】(1)作图见试题解析;(2)作图见试题解析,四边形AECF的形状为菱形.
【解析】
试题分析:先作以个角的交平分线,再作线段的垂直平分线得到几何图形,由AB=AC得∠ABC=∠ACB,由AM平分∠DAC得∠DAM=∠CAM,则利用三角形外角性质可得∠CAM=∠ACB,再根据线段垂直平分线的性质得OA=OC,∠AOF=∠COE,于是可证明△AOF≌△COE,所以OF=OE,然后根据菱形的判定方法易得四边形AECF的形状为菱形.
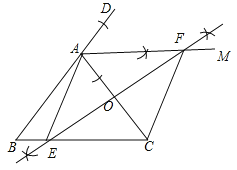
试题解析:解:如图所示,四边形AECF的形状为菱形.理由如下:
∵AB=AC,∴∠ABC=∠ACB,∵AM平分∠DAC,∴∠DAM=∠CAM,而∠DAC=∠ABC+∠ACB,∴∠CAM=∠ACB,∴EF垂直平分∠AC,∴OA=OC,∠AOF=∠COE,在△AOF和△COE中,∵∠FAO=∠ECO,OA=OC,∠AOF=∠COE,∴△AOF≌△COE,∴OF=OE,即AC和EF互相垂直平分,∴四边形AECF的形状为菱形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图1,抛物线![]() 与x轴交于点A(m﹣2,0)和B(2m+3,0)(点A在点B的左侧),与y轴交于点C,连结BC.
与x轴交于点A(m﹣2,0)和B(2m+3,0)(点A在点B的左侧),与y轴交于点C,连结BC.
(1)求m、n的值;
(2)如图2,点N为抛物线上的一动点,且位于直线BC上方,连接CN、BN.求△NBC面积的最大值;
(3)如图3,点M、P分别为线段BC和线段OB上的动点,连接PM、PC,是否存在这样的点P,使△PCM为等腰三角形,△PMB为直角三角形同时成立?若存在,求出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,工程队铺设一公路,他们从点A处铺设到点B处时,由于水塘挡路,他们决定改变方向经过点C,再拐到点D,然后沿着与AB平行的DE方向继续铺设,如果∠ABC=120°,∠CDE=140°,则∠BCD的度数是 . 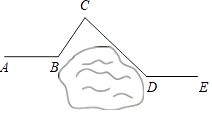
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,△ABC的顶点都在网格上,平移△ABC,使点C与坐标原点O重合.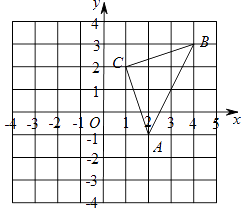
(1)请写出图中点A、B、C的坐标.
(2)画出平移后的△OA1B1 .
(3)求△OA1A的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,一次函数y=x与二次函数![]() 的图象相交于O、A两点,点A(3,3),点M为抛物线的顶点.
的图象相交于O、A两点,点A(3,3),点M为抛物线的顶点.
(1)求二次函数的表达式;
(2)长度为![]() 的线段PQ在线段OA(不包括端点)上滑动,分别过点P、Q作x轴的垂线交抛物线于点P1、Q1,求四边形PQQ1P1面积的最大值;
的线段PQ在线段OA(不包括端点)上滑动,分别过点P、Q作x轴的垂线交抛物线于点P1、Q1,求四边形PQQ1P1面积的最大值;
(3)直线OA上是否存在点E,使得点E关于直线MA的对称点F满足S△AOF=S△AOM?若存在,求出点E的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是∠AOB的边OB上的一点,过点P画OB的垂线,交OA于点C;
(1)①过点C画OB的平行线CD;②过点P画OA的垂线,垂足为H;
(2)线段PH的长度是点P到的距离,线段的长度是点C到直线OB的距离.线段PC、PH、OC这三条线段大小关系是(用“<”号连接).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com