
【题目】已知抛物线y=x2+(2m+1)x+m(m﹣3)(m为常数,﹣1≤m≤4).A(﹣m﹣1,y1),B( ![]() ,y2),C(﹣m,y3)是该抛物线上不同的三点,现将抛物线的对称轴绕坐标原点O逆时针旋转90°得到直线a,过抛物线顶点P作PH⊥a于H.
,y2),C(﹣m,y3)是该抛物线上不同的三点,现将抛物线的对称轴绕坐标原点O逆时针旋转90°得到直线a,过抛物线顶点P作PH⊥a于H.
(1)用含m的代数式表示抛物线的顶点坐标;
(2)若无论m取何值,抛物线与直线y=x﹣km(k为常数)有且仅有一个公共点,求k的值;
(3)当1<PH≤6时,试比较y1 , y2 , y3之间的大小.
【答案】
(1)
解:∵﹣ ![]() =﹣
=﹣ ![]() ,
, ![]() =
= ![]() =﹣
=﹣ ![]() ,
,
∴顶点坐标(﹣ ![]() ,﹣
,﹣ ![]() )
)
(2)
解:由 ![]() 消去y得x2+2mx+(m2+km﹣3m)=0,
消去y得x2+2mx+(m2+km﹣3m)=0,
∵抛物线与x轴有且仅有一个公共点,
∴△=0,即(k﹣3)m=0,
∵无论m取何值,方程总是成立,
∴k﹣3=0,
∴k=3
(3)
解:PH=|﹣ ![]() ﹣(﹣
﹣(﹣ ![]() )|=|
)|=| ![]() |,
|,
∵1<PH≤6,
∴当 ![]() >0时,有1<
>0时,有1< ![]() ≤6,又﹣1≤m≤4,
≤6,又﹣1≤m≤4,
∴ ![]() <m≤
<m≤ ![]() ,
,
当 ![]() <0时,1<﹣
<0时,1<﹣ ![]() ≤6,又∵﹣1≤m≤4,
≤6,又∵﹣1≤m≤4,
∴ ![]() ,
,
∴﹣1≤m<﹣ ![]() 或
或 ![]() <m≤
<m≤ ![]() ,
,
∵A(﹣m﹣1,y1)在抛物线上,
∴y1=(﹣m﹣1)2+(2m+1)(﹣m﹣1)+m(m+3)=﹣4m,
∵C(﹣m,y3)在抛物线上,
∴y3=(﹣m)2+(2m+1)(﹣m)+m(m﹣3)=﹣4m,
∴y1=y3,
①令 ![]() <﹣m﹣1,则有m<﹣
<﹣m﹣1,则有m<﹣ ![]() ,结合﹣1≤m≤﹣
,结合﹣1≤m≤﹣ ![]() ,
,
∴﹣1≤m<﹣ ![]() ,
,
此时,在对称轴的左侧y随x的增大而减小,如图1:
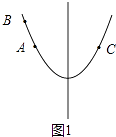 ,
,
∴y2>y1=y3,
即当﹣1≤m<﹣ ![]() 时,有y2>y1=y3.
时,有y2>y1=y3.
②令 ![]() =﹣m﹣1,则A与B重合,此情形不合题意,舍弃.
=﹣m﹣1,则A与B重合,此情形不合题意,舍弃.
③令 ![]() >﹣m﹣1,且
>﹣m﹣1,且 ![]() ≤﹣
≤﹣ ![]() 时,有﹣
时,有﹣ ![]() <m≤﹣
<m≤﹣ ![]() ,结合﹣1≤m<﹣
,结合﹣1≤m<﹣ ![]() ,
,
∴﹣ ![]() <m≤﹣
<m≤﹣ ![]() ,
,
此时,在对称轴的左侧,y随x的增大而减小,如图2:

∴y1=y3>y2,
即当﹣ ![]() <m≤﹣
<m≤﹣ ![]() 时,有y1=y3>y2,
时,有y1=y3>y2,
④令﹣ ![]() ≤
≤ ![]() <﹣m,有﹣
<﹣m,有﹣ ![]() ≤m<0,结合﹣1≤m<﹣
≤m<0,结合﹣1≤m<﹣ ![]() ,
,
∴﹣ ![]() ≤m<﹣
≤m<﹣ ![]() ,
,
此时,在对称轴的右侧y随x的增大而增大,如图3:

∴y2<y3=y1.
⑤令 ![]() =﹣m,B,C重合,不合题意舍弃.
=﹣m,B,C重合,不合题意舍弃.
⑥令 ![]() >﹣m,有m>0,结合
>﹣m,有m>0,结合 ![]() <m≤
<m≤ ![]() ,
,
∴ ![]() <m≤
<m≤ ![]() ,
,
此时,在对称轴的右侧,y随x的增大而增大,如图4:
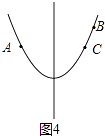
∴y2>y3=y1,
即当 ![]() <m≤
<m≤ ![]() 时,有y2>y3=y1,
时,有y2>y3=y1,
综上所述,﹣1≤m<﹣ ![]() 或
或 ![]() <m≤
<m≤ ![]() 时,有y2>y1=y3,
时,有y2>y1=y3,
﹣ ![]() <m<﹣
<m<﹣ ![]() 时,有y2<y1=y3.
时,有y2<y1=y3.
【解析】(1)根据顶点坐标公式即可解决问题.(2)列方程组根据△=0解决问题.(3)首先证明y1=y3 , 再根据点B的位置,分类讨论,①令 ![]() <﹣m﹣1,求出m的范围即可判断,②令
<﹣m﹣1,求出m的范围即可判断,②令 ![]() =﹣m﹣1,则A与B重合,此情形不合题意,舍弃.
=﹣m﹣1,则A与B重合,此情形不合题意,舍弃.
③令 ![]() >﹣m﹣1,求出m的范围即可判断,④令﹣
>﹣m﹣1,求出m的范围即可判断,④令﹣ ![]() ≤
≤ ![]() <﹣m,求出m的范围即可判断,⑤令
<﹣m,求出m的范围即可判断,⑤令 ![]() =﹣m,B,C重合,不合题意舍弃.⑥令
=﹣m,B,C重合,不合题意舍弃.⑥令 ![]() >﹣m,求出m的范围即可判断.本题考查二次函数综合题、顶点坐标公式等知识,解题的关键是熟练掌握利用根的判别式解决抛物线与直线的交点问题,学会分类讨论,学会利用函数图象判断函数值的大小,属于中考压轴题.
>﹣m,求出m的范围即可判断.本题考查二次函数综合题、顶点坐标公式等知识,解题的关键是熟练掌握利用根的判别式解决抛物线与直线的交点问题,学会分类讨论,学会利用函数图象判断函数值的大小,属于中考压轴题.
【考点精析】本题主要考查了二次函数的图象和二次函数的性质的相关知识点,需要掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=x2+bx+c经过点(0,﹣3),请你确定一个b的值,使该抛物线与x轴的一个交点在(1,0)和(3,0)之间.你确定的b的值是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某景点试开放期间,团队收费方案如下:不超过30人时,人均收费120元;超过30人且不超过m(30<m≤100)人时,每增加1人,人均收费降低1元;超过m人时,人均收费都按照m人时的标准.设景点接待有x名游客的某团队,收取总费用为y元.
(1)求y关于x的函数表达式;
(2)景点工作人员发现:当接待某团队人数超过一定数量时,会出现随着人数的增加收取的总费用反而减少这一现象.为了让收取的总费用随着团队中人数的增加而增加,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人都握有分别标记为A、B、C的三张牌,两人做游戏,游戏规则是:若两人出的牌不同,则A胜B,B胜C,C胜A;若两人出的牌相同,则为平局.
(1)用树状图或列表等方法,列出甲、乙两人一次游戏的所有可能的结果;
(2)求出现平局的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y= ![]() x+
x+ ![]() 与两坐标轴分别交于A、B两点.
与两坐标轴分别交于A、B两点. 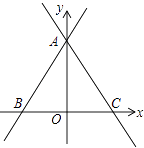
(1)求∠ABO的度数;
(2)过A的直线l交x轴半轴于C,AB=AC,求直线l的函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,M、N分别是AB、AC的中点,延长BC至点D,使CD= ![]() BD,连接DM、DN、MN.若AB=6,则DN= .
BD,连接DM、DN、MN.若AB=6,则DN= . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班数学兴趣小组利用数学活动课时间测量位于烈山山顶的炎帝雕像高度,已知烈山坡面与水平面的夹角为30°,山高857.5尺,组员从山脚D处沿山坡向着雕像方向前进1620尺到达E点,在点E处测得雕像顶端A的仰角为60°,求雕像AB的高度. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为保证中小学生每天锻炼一小时,某校开展了形式多样的体育活动项目,小明对某班同学参加锻炼的情况进行了统计,并绘制了下面的统计 图(1)和图(2).
(1)请根据所给信息在图(1)中将表示“乒乓球”项目的图形补充完整;
(2)扇形统计图(2)中表示”足球”项目扇形的圆心角度数为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,AC⊥AB,AB=2 ![]() ,AC=2,点D是以AB为直径的半圆O上一动点,DE⊥CD交直线AB于点E,设∠DAB=α(0°<α<90°).
,AC=2,点D是以AB为直径的半圆O上一动点,DE⊥CD交直线AB于点E,设∠DAB=α(0°<α<90°). 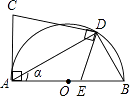
(1)当α=18°时,求 ![]() 的长;
的长;
(2)当α=30°时,求线段BE的长;
(3)若要使点E在线段BA的延长线上,则α的取值范围是(直接写出答案)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com