
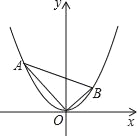
【题目】如图,点A(a,b)是抛物线![]() 上一动点,OB⊥OA交抛物线于点B(c,d).当点A在抛物线上运动的过程中(点A不与坐标原点O重合),以下结论:①ac为定值;②ac=﹣bd;③△AOB的面积为定值;④直线AB必过一定点.正确的有( )
上一动点,OB⊥OA交抛物线于点B(c,d).当点A在抛物线上运动的过程中(点A不与坐标原点O重合),以下结论:①ac为定值;②ac=﹣bd;③△AOB的面积为定值;④直线AB必过一定点.正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
【答案】C
【解析】分析:过点A、B分别作x轴的垂线,通过构建相似三角形以及函数解析式来判断①②是否正确.![]() 的面积不易直接求出,那么可由梯形的面积减去构建的两个直角三角形的面积得出,根据得出的式子判断这个面积是否为定值.利用待定系数法求出直线AB的解析式,即可判断④是否正确.
的面积不易直接求出,那么可由梯形的面积减去构建的两个直角三角形的面积得出,根据得出的式子判断这个面积是否为定值.利用待定系数法求出直线AB的解析式,即可判断④是否正确.
详解:过A.B分别作AC⊥x轴于C.BD⊥x轴于D,则:AC=b,OC=a,OD=c,BD=d;
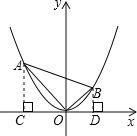
(1)由于OA⊥OB,易知△OAC∽△BOD,有:
![]() 即
即![]()
∴ac=bd(结论②正确).
(2)将点A.B的坐标代入抛物线的解析式中,有:
![]() …Ⅰ、
…Ⅰ、![]() …Ⅱ;
…Ⅱ;
Ⅰ×Ⅱ,得:![]() 即
即![]() (结论①正确).
(结论①正确).
(3)![]() ,
,
![]() ,
,
![]()
由此可看出,△AOB的面积不为定值(结论③错误).
(4)设直线AB的解析式为:y=kx+h,代入A.B的坐标,得:
ak+h=b…Ⅲ、ck+h=d…Ⅳ
Ⅲ×cⅣ×a,得:![]()
∴直线AB与y轴的交点为(0,2)(结论④正确).
综上,共有三个结论是正确的,它们是①②④,
故选C.


 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案科目:初中数学 来源: 题型:
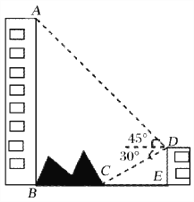
【题目】如图,大楼底右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为30°,测得大楼顶端A的仰角为45°(点B,C,E在同一水平直线上). 已知AB=80m,DE=10m,求障碍物B,C两点间的距离.(结果精确到0.1m)
(参考数据: ![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
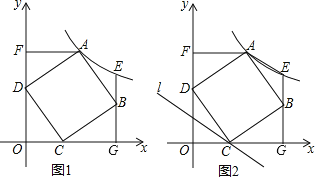
【题目】如图1,在平面直角坐标系中,正方形ABCD顶点C(3,0),顶点D(0,4),过点A作AF⊥y轴于F点,过点B作x轴的垂线交过A点的反比例函数y=![]() (k>0)的图象于E点,交x轴于G点.
(k>0)的图象于E点,交x轴于G点.
(1)求证:△CDO≌△DAF.
(2)求反比例函数解析式及点E的坐标;
(3)如图2,过点C作直线l∥AE,在直线l上是否存在一点P使△PAC是等腰三角形?若存在,求P点坐标,不存在说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
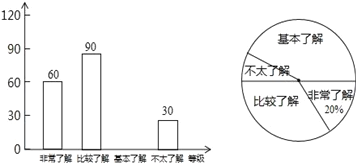
【题目】某校举行“足球在身边”的专题调查活动,采取随机抽样的方法进行问卷调查,调查结果划分为“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级,并将调查结果绘制成两幅不完整的统计图(如图),请根据图中提供的信息,解答下列问题:
(1)被调查的学生共有___人.在扇形统计图中,表示“比较了解”的扇形的圆心角度数为___度
(2)请用列表法或树状分析从![]() 名男生和
名男生和![]() 名女生中随机抽取
名女生中随机抽取![]() 名学生参加“足球在身边”的知识竞赛,抽中
名学生参加“足球在身边”的知识竞赛,抽中![]() 男
男![]() 女的概率.
女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
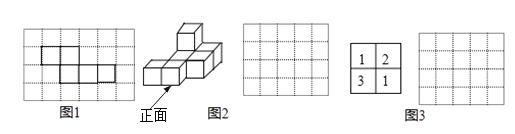
【题目】(1)小明准备制作一个封闭的正方体盒子,他先用5个大小一样的正方形制成如图1所示的拼接图形(实线部分),经折叠后发现还少一个面,请在图中的拼接图形上再接一个正方形,使新拼接的图形经过折叠后能成为一个封闭的正方体盒子.(添加的正方形用阴影表示.只要画出一种即可)
(2)如图2所示的几何体是由几个相同的正方体搭成的,请画出它从正面看的形状图.
(3)如图3是几个正方体所组成的几何体从上面看的形状图,小正方形中的数字表示该位置小正方体的个数,请画出这个几何体从左面看的形状图.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一批电视机,一月份每台毛利润是售出价的20%(毛利润=售出价-买入价),二月份该商场将每台售出价调低10%(买入价不变),结果销售台数比一月份增加120%,那么二月份的毛利润总额与一月份毛利润总额的比是__________。
查看答案和解析>>
科目:初中数学 来源: 题型:
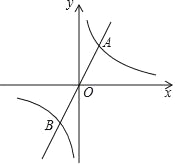
【题目】如图,已知正比例函数y=2x与反比例函数y=![]() (k>0)的图象交于A、B两点,且点A的横坐标为4,
(k>0)的图象交于A、B两点,且点A的横坐标为4,
(1)求k的值;
(2)根据图象直接写出正比例函数值小于反比例函数值时x的取值范围;
(3)过原点O的另一条直线l交双曲线y=![]() (k>0)于P、Q两点(P点在第一象限),若由点A、P、B、Q为顶点组成的四边形面积为224,求点P的坐标.
(k>0)于P、Q两点(P点在第一象限),若由点A、P、B、Q为顶点组成的四边形面积为224,求点P的坐标.
【答案】(1) k=32 (2) x<﹣8或0<x<8 (3) P(﹣7+3![]() ,16+
,16+![]() );或P(7+3
);或P(7+3![]() ,﹣16+
,﹣16+![]() )
)
【解析】分析:(1)先将x=4代入正比例函数y=2x,可得出y=8,求得点A(4,8),再根据点A与B关于原点对称,得出B点坐标,即可得出k的值;
(2)正比例函数的值小于反比例函数的值即正比例函数的图象在反比例函数的图象下方,根据图形可知在交点的右边正比例函数的值小于反比例函数的值.
(3)由于双曲线是关于原点的中心对称图形,因此以A、B、P、Q为顶点的四边形应该是平行四边形,那么△POA的面积就应该是四边形面积的四分之一即56.可根据双曲线的解析式设出P点的坐标,然后表示出△POA的面积,由于△POA的面积为56,由此可得出关于P点横坐标的方程,即可求出P点的坐标.
详解:(1)∵点A在正比例函数y=2x上,
∴把x=4代入正比例函数y=2x,
解得y=8,∴点A(4,8),
把点A(4,8)代入反比例函数y=![]() ,得k=32,
,得k=32,
(2)∵点A与B关于原点对称,
∴B点坐标为(﹣4,﹣8),
由交点坐标,根据图象直接写出正比例函数值小于反比例函数值时x的取值范围,x<﹣8或0<x<8;
(3)∵反比例函数图象是关于原点O的中心对称图形,
∴OP=OQ,OA=OB,
∴四边形APBQ是平行四边形,
∴S△POA=S平行四边形APBQ×=![]() ×224=56,
×224=56,
设点P的横坐标为m(m>0且m≠4),
得P(m, ![]() ),
),
过点P、A分别做x轴的垂线,垂足为E、F,
∵点P、A在双曲线上,
∴S△POE=S△AOF=16,
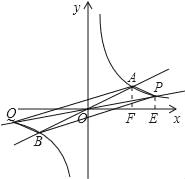
若0<m<4,如图,
∵S△POE+S梯形PEFA=S△POA+S△AOF,
∴S梯形PEFA=S△POA=56.
∴![]() (8+
(8+![]() )(4﹣m)=56.
)(4﹣m)=56.
∴m1=﹣7+3![]() ,m2=﹣7﹣3
,m2=﹣7﹣3![]() (舍去),
(舍去),
∴P(﹣7+3![]() ,16+
,16+![]() );
);
若m>4,如图,
∵S△AOF+S梯形AFEP=S△AOP+S△POE,
∴S梯形PEFA=S△POA=56.
∴![]() ×(8+
×(8+![]() )(m﹣4)=56,
)(m﹣4)=56,
解得m1=7+3![]() ,m2=7﹣3
,m2=7﹣3![]() (舍去),
(舍去),
∴P(7+3![]() ,﹣16+
,﹣16+![]() ).
).
∴点P的坐标是P(﹣7+3![]() ,16+
,16+![]() );或P(7+3
);或P(7+3![]() ,﹣16+
,﹣16+![]() ).
).

点睛:本题考查了待定系数法求反比例函数与一次函数的解析式和反比例函数y=![]() 中k的几何意义.这里体现了数形结合的思想,做此类题一定要正确理解k的几何意义.利用数形结合的思想,求得三角形的面积.
中k的几何意义.这里体现了数形结合的思想,做此类题一定要正确理解k的几何意义.利用数形结合的思想,求得三角形的面积.
【题型】解答题
【结束】
23
【题目】如图,在梯形ABCD中,AD∥BC,AB=DC=AD=9,∠ABC=70°,点E,F分别在线段AD,DC上(点E与点A,D不重合),且∠BEF=110°.
(1)求证:△ABE∽△DEF.
(2)当点E为AD中点时,求DF的长;
(3)在线段AD上是否存在一点E,使得F点为CD的中点?若存在,求出AE的长度;若不存在,试说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com