
【题目】如图,一次函数y1=k1x+b(k1、b为常数,k1≠0)的图象与反比例函数y2=![]() (k2≠0)的图象交于点A(m,1)与点B(﹣1,﹣4).
(k2≠0)的图象交于点A(m,1)与点B(﹣1,﹣4).
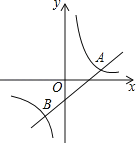
(1)求反比例函数与一次函数的解析式;
(2)根据图象说明,当x为何值时,k1x+b﹣![]() <0;
<0;
(3)若动点P是第一象限内双曲线上的点(不与点A重合),连接OP,过点P作y轴的平行线交直线AB于点C,连接OC,若△POC的面积为3,求点P的坐标.
【答案】(1)y1=x﹣3;![]() ;(2)x<﹣1或0<x<4;(3)点P的坐标为
;(2)x<﹣1或0<x<4;(3)点P的坐标为![]() 或(1,4)或(2,2)
或(1,4)或(2,2)
【解析】
(1)把B点坐标代入反比例函数解析式可求得k2的值,把点A(m,1)代入求得的反比例函数的解析式求得m,然后利用待定系数法即可求得一次函数的解析式;
(2)直接由A、B的坐标根据图象可求得答案;
(3)设点P的坐标为![]() ,则C(m,m﹣3),由△POC的面积为3,得到△POC的面积
,则C(m,m﹣3),由△POC的面积为3,得到△POC的面积![]() ,求得m的值,即可求得P点的坐标.
,求得m的值,即可求得P点的坐标.
解:(1)将B(﹣1,﹣4)代入![]() 得:k2=4
得:k2=4
∴反比例函数的解析式为![]() ,
,
将点A(m,1)代入y2得![]() ,解得m=4,
,解得m=4,
∴A(4,1)
将A(4,1)、B(﹣1,﹣4)代入一次函数y1=k1x+b得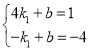
解得k1=1,b=﹣3
∴一次函数的解析式为y1=x﹣3;
(2)由图象可知:x<﹣1或0<x<4时,k1x+b﹣![]() <0;
<0;
(3)如图:设点P的坐标为![]() ,则C(m,m﹣3)
,则C(m,m﹣3)
∴![]() ,点O到直线PC的距离为m
,点O到直线PC的距离为m
∴△POC的面积=![]() ,
,
解得:m=5或﹣2或1或2,
又∵m>0
∴m=5或1或2,
∴点P的坐标为![]() 或(1,4)或(2,2).
或(1,4)或(2,2).



 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:初中数学 来源: 题型:
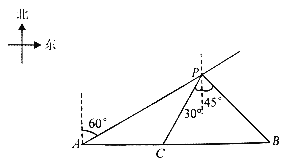
【题目】近日,国产航母山东舰成为了新晋网红,作为我国本世纪建造的第一艘真正意义上的国产航母,承载了我们太多期盼,促使我国在伟大复兴路上加速前行如图,山东舰在一次测试中,巡航到海岛A北偏东60°方向P处,发现在海岛A正东方向有一可疑船只B正沿BA方向行驶。山东舰经测量得出:可疑船只在P处南偏东45°方向,距P处![]() 海里。山东舰立即从P沿南偏西30°方向驶出,刚好在C处成功拦截可疑船只。求被拦截时,可疑船只距海岛A还有多少海里?(
海里。山东舰立即从P沿南偏西30°方向驶出,刚好在C处成功拦截可疑船只。求被拦截时,可疑船只距海岛A还有多少海里?(![]() ,结果精确到0.1海里)
,结果精确到0.1海里)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大学生利用业余时间参与了一家网店经营,销售一种成本为30元/件的文化衫,根据以往的销售经验,他整理出这种文化衫的售价y1(元/件),销量y2(件)与第x(1≤x<90)天的函数图象如图所示(销售利润=(售价-成本)×销量).
(1)求y1与y2的函数解析式.
(2)求每天的销售利润W与x的函数解析式.
(3)销售这种文化衫的第多少天,销售利润最大,最大利润是多少?


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,小刚家,菜地,稻田在同一条直线上.小刚从家去菜地浇水,又去稻田除草,然后回家.如图反映了这个过程中,小刚离家的距离y与时间x之间的对应关系.如果菜地和稻田的距离为akm,小刚在稻田除草比在菜地浇水多用了bmin,则a,b的值分别为( )
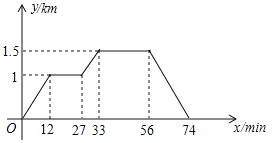
A.1,8B.0.5,12C.1,12D.0.5,8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,并且关于x的一元二次方程ax2+bx+c﹣m=0有两个不相等的实数根,下列结论:其中,正确的个数有( )
①b2﹣4ac<0;②a﹣b+c<0;③abc>0;④m>﹣2.
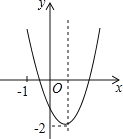
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的盒子中放入四张卡片,每张卡片上都写有一个数字,分别是2,1,0,1.卡片除数字不同外其它均相同,从中随机抽取两张卡片,抽取的两张卡片上数字之积为 0的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
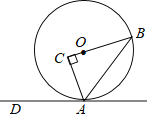
【题目】如图,以⊙O的弦AB为斜边作Rt△ABC,C点在圆内,边BC经过圆心O,过A点作⊙O的切线AD.
(1)求证:∠DAC=2∠B;
(2)若sinB=![]() ,AC=6,求⊙O的半径.
,AC=6,求⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com