
【题目】如图,在平面直角坐标系xOy中,一次函数y1=ax+b的图象与反比例函数y2![]() 的图象相交于点A(﹣4,﹣2),B(m,4).
的图象相交于点A(﹣4,﹣2),B(m,4).
(1)求反比例函数和一次函数的表达式;
(2)观察图象,写出使得y1>y2成立的自变量x的取值范围.
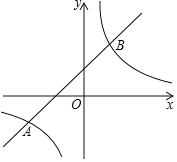
【答案】(1)y1=x+2,y2![]() ;(2)﹣4<x<0或x>2.
;(2)﹣4<x<0或x>2.
【解析】
(1)先把A点坐标代入反比例函数中即可求出反比例函数的表达式,然后根据反比例函数的表达式求出B的坐标,再将A,B的坐标代入一次函数中即可求出一次函数的表达式;
(2)根据图象及反比例函数与一次函数的交点即可得出答案.
(1)把A(﹣4,﹣2)代入y2![]() 得到k=8,
得到k=8,
∴反比例函数表达式y2![]() ,
,
把B(m,4)代入y2![]() ,得到m=2,
,得到m=2,
∴B(2,4),
把A、B的坐标代入y1=ax+b,
则有![]() ,解得
,解得![]() ,
,
∴一次函数表达式y1=x+2.
(2)观察图象可知,y1![]() y2时一次函数在反比例上方,
y2时一次函数在反比例上方,
∴使得y1![]() y2成立的自变量x的取值范围:﹣4<x<0或x>2.
y2成立的自变量x的取值范围:﹣4<x<0或x>2.


科目:初中数学 来源: 题型:
【题目】关于反比例函数y=﹣![]() ,下列说法错误的是( )
,下列说法错误的是( )
A.图象经过点(1,﹣3)
B.图象分布在第一、三象限
C.图象关于原点对称
D.图象与坐标轴没有交点
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在菱形![]() 中,
中,![]() ,点
,点![]() 是对角线
是对角线![]() 上一动点,将线段
上一动点,将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 到
到![]() ,连接
,连接![]() .
.
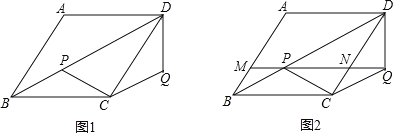
(1)如图1,求证:![]() ;
;
(2)如图2,连接![]() 并延长,分别交
并延长,分别交![]() 、
、![]() 于点
于点![]() 、
、![]() .
.
①求证:![]() ;②若
;②若![]() 的最小值为
的最小值为![]() ,直接写出菱形
,直接写出菱形![]() 的面积为 .
的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有甲、乙、丙三个不透明的布袋,甲袋中装有2个相同的小球,它们分别标有字母A和B;乙袋中装有3个相同的小球,它们分别标有字母C、D和E;丙袋中装有2个相同的小球,它们分别标有字母H和I.从三个布袋中各随机取出一个小球.求:(1)取出的3个小球恰好有2个元音字母的概率;(2)取出的3个小球全是辅音字母的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
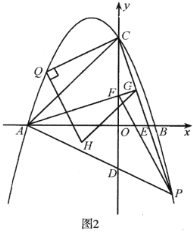
【题目】在平面直角坐标系中,点![]() 为坐标原点,抛物线
为坐标原点,抛物线![]() 交
交![]() 轴的负半轴于点
轴的负半轴于点![]() ,交
,交![]() 轴的正半轴于点
轴的正半轴于点![]() ,交
,交![]() 轴于点
轴于点![]() ,且
,且![]() .
.
![]() 求
求![]() 的值;
的值;
![]() 如图1,点
如图1,点![]() 在第四象限的抛物线上,横坐标为
在第四象限的抛物线上,横坐标为![]() 连接
连接![]() ,交
,交![]() 轴于点
轴于点![]() ,设
,设![]() ,求
,求![]() 与
与![]() 之间的函数关系式,并直接写出自变量
之间的函数关系式,并直接写出自变量![]() 的取值范围;
的取值范围;

![]() 如图2,在
如图2,在![]() 的条件下,连接
的条件下,连接![]() ,交
,交![]() 轴于点
轴于点![]() ,点
,点![]() 在线段
在线段![]() 上,射线
上,射线![]() 交
交![]() 于点
于点![]() ,点
,点![]() 在第二象限的抛物线上,连接
在第二象限的抛物线上,连接![]() ,将线段
,将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到线段
得到线段![]() ,连接
,连接![]() ,若
,若![]() ,
,![]() ,求点
,求点![]() 和
和![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋子中装有四个小球,上面分别标有数字﹣2,﹣1,0,1,它们除了数字不同外,其它完全相同.
(1)随机从袋子中摸出一个小球,摸出的球上面标的数字为正数的概率是 .
(2)小聪先从袋子中随机摸出一个小球,记下数字作为平面直角坐标系内点M的横坐标;然后放回搅匀,接着小明从袋子中随机摸出一个小球,记下数字作为点M的纵坐标.如图,已知四边形ABCD的四个顶点的坐标分别为A(﹣2,0),B(0,﹣2),C(1,0),D(0,1),请用画树状图或列表法,求点M落在四边形ABCD所围成的部分内(含边界)的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某体育老师统计了七年级甲、乙两个班女生的身高,并绘制了以下不完整的统计图.

请根据图中信息,解决下列问题:
(1)两个班共有女生多少人?
(2)将频数分布直方图补充完整;
(3)求扇形统计图中![]() 部分所对应的扇形圆心角度数;
部分所对应的扇形圆心角度数;
(4)身高在![]() 的5人中,甲班有3人,乙班有2人,现从中随机抽取两人补充到学校国旗队.请用列表法或画树状图法,求这两人来自同一班级的概率.
的5人中,甲班有3人,乙班有2人,现从中随机抽取两人补充到学校国旗队.请用列表法或画树状图法,求这两人来自同一班级的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c与x轴交于A(1,0),B(﹣3,0)两点.

(1)求该抛物线的解析式;
(2)设(1)中的抛物线交y轴与C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由;
(3)在(1)中的抛物线上的第二象限上是否存在一点P,使△PBC的面积最大?若存在,求出点P的坐标及△PBC的面积最大值;若没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
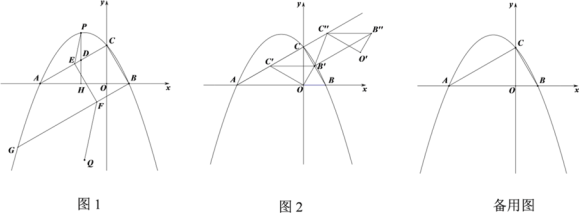
【题目】如图,在平面直角坐标系中,抛物线![]() 与x轴交于A、B两点(点A在点B左侧),与y轴交于点C,OB=1,∠OBC=60°.
与x轴交于A、B两点(点A在点B左侧),与y轴交于点C,OB=1,∠OBC=60°.
(1)如图1,求直线BC的解析式;
(2)如图1,线段AC上方抛物线上有一动点P,PD⊥x轴于点H,交线段AC于点D,直线BG∥AC,交抛物线于点G,点F是直线BC上一动点,FE∥BC交AC于点E,点Q是点A关于直线BG的对称点,连接PE、QF.当线段PD取最大值时,求PE+EF+QF的最小值及点E的坐标;
(3)如图2,将△BOC绕点O逆时针旋转至△B′O C′的位置,点B、C的对应点分别为点B′、C′,点B′恰好落在BC上.将△B′O C′沿直线AC平移,得到△B′′O ′ C′′,点B′、C′、O的对应点分别为点B′′、C′′、O ′,连接B ′ B′′、B ′C′′,△B ′B′′C′′是否能为等腰三角形?若能,请直接写出所有符合条件的C′′的坐标;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com