
【题目】在菱形![]() 中,
中,![]() ,点
,点![]() 是对角线
是对角线![]() 上一动点,将线段
上一动点,将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 到
到![]() ,连接
,连接![]() .
.
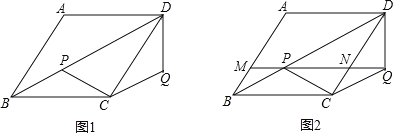
(1)如图1,求证:![]() ;
;
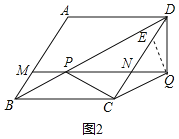
(2)如图2,连接![]() 并延长,分别交
并延长,分别交![]() 、
、![]() 于点
于点![]() 、
、![]() .
.
①求证:![]() ;②若
;②若![]() 的最小值为
的最小值为![]() ,直接写出菱形
,直接写出菱形![]() 的面积为 .
的面积为 .
【答案】(1)见解析;(2)①见解析;②![]()
【解析】
(1)由菱形的性质得出BC=DC,∠BCD=120°,由旋转的性质得PC=QC,∠PCQ=120°,得出∠BCP=∠DCQ,由SAS得出△BCP≌△DCQ即可;
(2)①由全等三角形的性质得出BP=DQ,得出∠QDC=∠PBC=∠PBM=30°,在CD上取点E,使QE=QN,则∠QEN=∠QNE,得出∠QED=∠QNC=∠PMB,证明△PBM≌△QDE(AAS),即可得出结论;
②由①知PM=QN,得出MN=PQ=![]() PC,当PC⊥BD时,此时MN最小,则PC=2,BC=2PC=4,菱形ABCD的面积=2△ABC的面积,即可得出答案.
PC,当PC⊥BD时,此时MN最小,则PC=2,BC=2PC=4,菱形ABCD的面积=2△ABC的面积,即可得出答案.
证明:(1)四边形![]() 是菱形,
是菱形,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]()
由旋转的性质得:![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,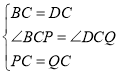 ,
,
![]() ;
;
(2)①证明:由(1)得:![]() ,
,
![]() ,
,
![]() .
.
在![]() 上取点
上取点![]() ,使
,使![]() ,如图2所示:
,如图2所示:
则![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,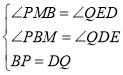 ,
,
![]()
![]() ,
,
![]() .
.
②解:由①知![]() ,
,
![]() ,
,
![]() 当
当![]() 时,
时,![]() 最小,此时
最小,此时![]() 最小,
最小,
则![]() ,
,![]() ,
,
![]() 菱形
菱形![]() 的面积
的面积![]() .
.
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】若抛物线![]() (a、b、c是常数,
(a、b、c是常数, ![]() )与直线
)与直线![]() 都经过
都经过![]() 轴上的一点P,且抛物线L的顶点Q在直线
轴上的一点P,且抛物线L的顶点Q在直线![]() 上,则称此直线
上,则称此直线![]() 与该抛物线L具有“一带一路”关系,此时,直线
与该抛物线L具有“一带一路”关系,此时,直线![]() 叫做抛物线L的“带线”,抛物线L叫做直线
叫做抛物线L的“带线”,抛物线L叫做直线![]() 的“路线”.
的“路线”.
(1)若直线![]() 与抛物线
与抛物线![]() 具有“一带一路”关系,求m、n的值.
具有“一带一路”关系,求m、n的值.
(2)若某“路线”L的顶点在反比例函数![]() 的图象上,它的“带线” 的解析式为
的图象上,它的“带线” 的解析式为![]() ,求此路的解析式.
,求此路的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
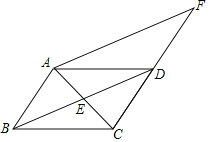
【题目】如图,在四边形ABCD中,AD∥BC,AC与BD交于点E,点E是BD的中点,延长CD到点F,使DF=CD,连接AF,
(1)求证:AE=CE;
(2)求证:四边形ABDF是平行四边形;
(3)若AB=2,AF=4,∠F=30°,则四边形ABCF的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某养鸡场有2500只鸡准备对外出售,从中随机抽取了一部分鸡,根据它们的质量(单位:kg),绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:
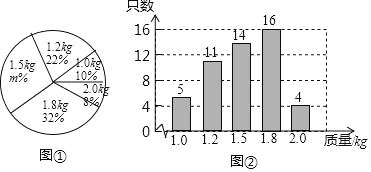
(1)图①中m的值为 ;
(2)这组数据的平均数是 kg,众数是 kg,中位数是 kg;
(3)根据样本数据,估计这2500只鸡中,质量为2.0kg的约有多少只?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】制作一种产品,需先将材料加热达到60 ℃后,再进行操作.设该材料温度为y(℃),从加热开始计算的时间为x(min).据了解,当该材料加热时,温度y与时间x成一次函数关系;停止加热进行操作时,温度y与时间x成反比例关系(如图).已知该材料在操作加热前的温度为15 ℃,加热5分钟后温度达到60 ℃.

(1)分别求出将材料加热和停止加热进行操作时,y与x的函数关系式;
(2)根据工艺要求,当材料的温度低于15 ℃时,须停止操作,那么从开始加热到停止操作,共经历了多少时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】期中考试中,A,B,C,D,E五位同学的数学、英语成绩有如表信息:
A | B | C | D | E | 平均分 | 中位数 | |
数学 | 71 | 72 | 69 | 68 | 70 |
|
|
英语 | 88 | 82 | 94 | 85 | 76 |
|
|
(1)完成表格中的数据;
(2)为了比较不同学科考试成绩的好与差,采用标准分是一个合理的选择,标准分的计算公式是:标准分=(个人成绩﹣平均成绩)÷成绩方差.
从标准分看,标准分高的考试成绩更好,请问A同学在本次考试中,数学与英语哪个学科考得更好?
查看答案和解析>>
科目:初中数学 来源: 题型:
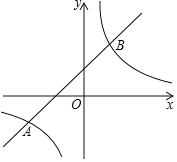
【题目】如图,在平面直角坐标系xOy中,一次函数y1=ax+b的图象与反比例函数y2![]() 的图象相交于点A(﹣4,﹣2),B(m,4).
的图象相交于点A(﹣4,﹣2),B(m,4).
(1)求反比例函数和一次函数的表达式;
(2)观察图象,写出使得y1>y2成立的自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形EFGH的顶点E,G分别在菱形ABCD的边AD,BC上,顶点F,H在菱形ABCD的对角线BD上.

(1)求证:BG=DE;
(2)若E为AD中点,FH=2,求菱形ABCD的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com