
【题目】已知抛物线与x轴交于A(6,0)、B(![]() ,0)两点,与y轴交于点C,过抛物线上点M(1,3)作MN⊥x轴于点N,连接OM.
,0)两点,与y轴交于点C,过抛物线上点M(1,3)作MN⊥x轴于点N,连接OM.
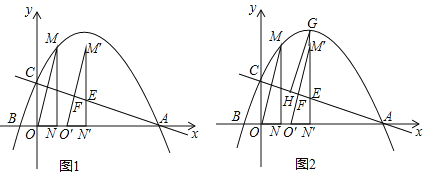
(1)求此抛物线的解析式;
(2)如图1,将△OMN沿x轴向右平移t个单位(0≤t≤5)到△O′M′N′的位置,MN′、M′O′与直线AC分别交于点E、F.
①当点F为M′O′的中点时,求t的值;
②如图2,若直线M′N′与抛物线相交于点G,过点G作GH∥M′O′交AC于点H,试确定线段EH是否存在最大值?若存在,求出它的最大值及此时t的值;若不存在,请说明理由.
【答案】(1)![]() ;(2)①1;②t=2时,EH最大值为
;(2)①1;②t=2时,EH最大值为![]() .
.
【解析】
试题分析:(1)设抛物线解析式为![]() ,把点M(1,3)代入即可求出a,进而解决问题.
,把点M(1,3)代入即可求出a,进而解决问题.
(2))①如图1中,AC与OM交于点G.连接EO′,首先证明△AOC∽△MNO,推出OM⊥AC,在RT△EO′M′中,利用勾股定理列出方程即可解决问题.
②由△GHE∽△AOC得![]() =
=![]() =
=![]() ,所以EG最大时,EH最大,构建二次函数求出EG的最大值即可解决问题.
,所以EG最大时,EH最大,构建二次函数求出EG的最大值即可解决问题.
试题解析:(1)设抛物线解析式为![]() ,把点M(1,3)代入得a=
,把点M(1,3)代入得a=![]() ,∴抛物线解析式为
,∴抛物线解析式为![]() ,∴
,∴![]() .
.
(2)①如图1中,AC与OM交于点G.连接EO′.∵AO=6,OC=2,MN=3,ON=1,∴![]() =3,∴
=3,∴![]() ,∵∠AOC=∠MON=90°,∴△AOC∽△MNO,∴∠OAC=∠NMO,∵∠NMO+∠MON=90°,∴∠MON+∠OAC=90°,∴∠AGO=90°,∴OM⊥AC,∵△M′N′O′是由△MNO平移所得,∴O′M′∥OM,∴O′M′⊥AC,∵M′F=FO′,∴EM′=EO′,∵EN′∥CO,∴
,∵∠AOC=∠MON=90°,∴△AOC∽△MNO,∴∠OAC=∠NMO,∵∠NMO+∠MON=90°,∴∠MON+∠OAC=90°,∴∠AGO=90°,∴OM⊥AC,∵△M′N′O′是由△MNO平移所得,∴O′M′∥OM,∴O′M′⊥AC,∵M′F=FO′,∴EM′=EO′,∵EN′∥CO,∴![]() ,∴
,∴![]() ,∴EN′=
,∴EN′=![]() (5﹣t),在RT△EO′M′中,∵O′N′=1,EN′=
(5﹣t),在RT△EO′M′中,∵O′N′=1,EN′=![]() (5﹣t),EO′=EM′=
(5﹣t),EO′=EM′=![]() ,∴
,∴![]() ,∴t=1.
,∴t=1.
②如图2中,∵GH∥O′M′,O′M′⊥AC,∴GH⊥AC,∴∠GHE=90°,∵∠EGH+∠HEG=90°,∠AEN′+∠OAC=90°,∠HEG=∠AEN′,∴∠OAC=∠HGE,∵∠GHE=∠AOC=90°,∴△GHE∽△AOC,∴![]() ,∴EG最大时,EH最大,∵EG=GN′﹣EN′=
,∴EG最大时,EH最大,∵EG=GN′﹣EN′=![]() =
=![]() =
=![]() ,∴t=2时,EG最大值=
,∴t=2时,EG最大值=![]() ,∴EH最大值=
,∴EH最大值=![]() ,∴t=2时,EH最大值为
,∴t=2时,EH最大值为![]() .
.


 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:初中数学 来源: 题型:
【题目】某景点试开放期间,团队收费方案如下:不超过30人时,人均收费120元;超过30人且不超过m(30<m≤100)人时,每增加1人,人均收费降低1元;超过m人时,人均收费都按照m人时的标准.设景点接待有x名游客的某团队,收取总费用为y元.
(1)求y关于x的函数表达式;
(2)景点工作人员发现:当接待某团队人数超过一定数量时,会出现随着人数的增加收取的总费用反而减少这一现象.为了让收取的总费用随着团队中人数的增加而增加,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
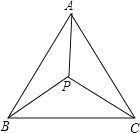
【题目】如图5,点P在正△ABC内一点,∠APB=125°, ∠BPC=100°,则以AP,BP,CP为边长的三角形各内角的度数为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点P、Q分别是等边△ABC边AB、BC上的动点(端点除外),点P从顶点A、点Q从顶点B同时出发,且它们的运动速度相同,连接AQ、CP交于点M.
(1)求证:△ABQ≌△CAP;
(2)当点P、Q分别在AB、BC边上运动时,∠QMC变化吗?若变化,请说明理由;若不变,求出它的度数.
(3)如图2,若点P、Q在运动到终点后继续在射线AB、BC上运动,直线AQ、CP交点为M,则∠QMC变化吗?若变化,请说明理由;若不变,直接写出它的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
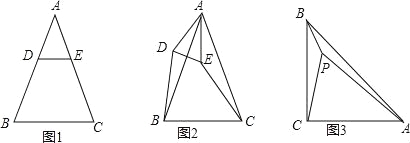
【题目】已知△ABC是等腰三角形,AB=AC.
(1)特殊情形:如图1,当DE∥BC时,有DB EC.(填“>”,“<”或“=”)
(2)发现探究:若将图1中的△ADE绕点A顺时针旋转α(0°<α<180°)到图2位置,则(1)中的结论还成立吗?若成立,请给予证明;若不成立,请说明理由.
(3)拓展运用:如图3,P是等腰直角三角形ABC内一点,∠ACB=90°,且PB=1,PC=2,PA=3,求∠BPC的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com