
【题目】如图所示,![]() ,
,![]() ,以
,以![]() 为圆心,
为圆心,![]() 长为半径画弧,与射线
长为半径画弧,与射线![]() 相交于点
相交于点![]() ,连接
,连接![]() ,过
,过![]() 作
作![]() 于点
于点![]() .
.
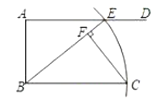
(1)线段![]() 与图中哪条线段相等?写出来并加以证明;
与图中哪条线段相等?写出来并加以证明;
(2)若![]() ,
,![]() ,
,![]() 从
从![]() 沿
沿![]() 方向运动,
方向运动,![]() 从
从![]() 出发向
出发向![]() 运动,两点同时出发且速度均为每秒1个单位.
运动,两点同时出发且速度均为每秒1个单位.
①当![]() _____秒时,四边形
_____秒时,四边形![]() 是矩形;
是矩形;
②当![]() _____秒时,四边形
_____秒时,四边形![]() 是菱形.
是菱形.
科目:初中数学 来源: 题型:
【题目】炎热的夏天来临之际.为了调查我校学生消防安全知识水平,学校组织了一次全校的消防安全知识培训,培训完后进行测试,在全校2400名学生中,分别抽取了男生,女生各15份成绩,整理分析过程如下,请补充完整.
(收集数据)
男生15名学生测试成绩统计如下:
68,72,89,85,82,85,74,92,80,85,76,85,69,78,80
女生15名学生测试成绩统计如下:(满分100分)
82,88,83,76,73,78,67,81,82,80,80,86,82,80,82
按如下分数段整理、描述这两组样本数据:
组别 频数 | 65.5~70.5 | 70.5~75.5 | 75.5~80.5 | 80.5~85.5 | 85.5~90.5 | 90.5~95.5 |
男生 | 2 | 2 | 4 | 5 | 1 | 1 |
女生 | 1 | 1 | 5 | 6 | 2 | 0 |
(分析数据)
(1)两组样本数据的平均数、众数、中位数、方差如下表所示:
班级 | 平均数 | 众数 | 中位数 | 方差 |
男生 | 80 | x | 80 | 45.9 |
女生 | 80 | 82 | y | 24.3 |
在表中:x=_____;y=_____.
(2)若规定得分在80分以上(不含80分)为合格,请估计全校学生中消防安全知识合格的学生有______人.
(3)通过数据分析得到的结论是女生掌握消防安全相关知识的整体水平比男生好,请从两个方面说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣x2+bx+c的图象经过点A(﹣1,0),C(0,3).
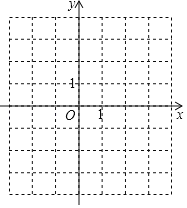
(1)求二次函数的解析式;
(2)在图中,画出二次函数的图象;
(3)根据图象,直接写出当y≤0时,x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小红家的阳台上放置了一个晒衣架如图①.图②是晒衣架的侧面示意图,立杆AB,CD相交于点O,B,D两点立于地面.经测量:AB=CD=136 cm,OA=OC=51 cm,OE=OF=34 cm,现将晒衣架完全稳固张开,扣链EF成一条线段,且EF=32 cm.垂挂在衣架上的连衣裙总长度小于________cm时,连衣裙才不会拖落到地面上.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某校数学兴趣小组为测量校园主教学楼AB的高度,由于教学楼底部不能直接到达,故兴趣小组在平地上选择一点C,用测角器测得主教学楼顶端A的仰角为30°,再向主教学楼的方向前进24米,到达点E处(C,E,B三点在同一直线上),又测得主教学楼顶端A的仰角为60°,已知测角器CD的高度为1.6米,请计算主教学楼AB的高度.(![]() ≈1.73,结果精确到0.1米)
≈1.73,结果精确到0.1米)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx向上平移2个单位之后,正好与x轴交于A(-3,0),B(1,0)两点,与y轴交于点C.
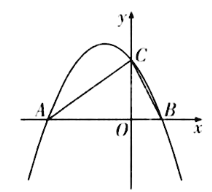
(1)求平移后抛物线的表达式;
(2)点Q是直线AC上方的抛物线上一点,过点Q作QE垂直于x轴,若以点B、Q、E为顶点的角形与△AOC相似,请求出Q点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,PA、PB、CD分别切⊙O于点A、B、E,CD分别交PA、PB于点C、D.下列关系:①PA=PB;②∠ACO=∠DCO;③∠BOE和∠BDE互补;④△PCD的周长是线段PB长度的2倍.则其中说法正确的有
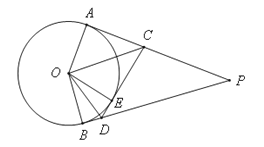
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
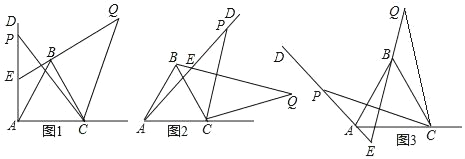
【题目】如图1,已知∠DAC=90°,△ABC是等边三角形,点P为射线AD上任意一点(点P与点A不重合),连结CP,将线段CP绕点C顺时针旋转60°得到线段CQ,连结QB并延长交直线AD于点E.
(1)如图1,猜想∠QEP= °;
(2)如图2,3,若当∠DAC是锐角或钝角时,其它条件不变,猜想∠QEP的度数,选取一种情况加以证明;
(3)如图3,若∠DAC=135°,∠ACP=15°,且AC=4,求BQ的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com