
【题目】如图,在平面直角坐标系中,点A1,A2,A3…都在x轴上,点B1,B2,B3…都在直线![]() 上,△OA1B1,△B1A1A2,△B2B1A2,△B2A2A3,△B3B2A3…都是等腰直角三角形,且OA1=1,则点B2019的坐标是_________________.
上,△OA1B1,△B1A1A2,△B2B1A2,△B2A2A3,△B3B2A3…都是等腰直角三角形,且OA1=1,则点B2019的坐标是_________________.

【答案】( 22018,22018)
【解析】
根据OA1=1,可得点A1的坐标为(1,0),然后根据△OA1B1,△B1A1A2,△B2B1A2,△B2A2A3,△B3B2A3…都是等腰直角三角形,求出A1A2,B1A2,A2A3,B2A3…的长度,然后找出规律,求出点B2019的坐标.
∵OA1=1,∴点A1的坐标为(1,0).
∵△OA1B1是等腰直角三角形,∴A1B1=1,∴B1(1,1).
∵△B1A1A2是等腰直角三角形,∴A1A2=1,B1A2![]() .
.
∵△B2B1A2为等腰直角三角形,∴A2A3=2,∴B2(2,2),同理可得:B3(22,22),B4(23,23),…Bn(2n﹣1,2n﹣1),∴点B2019的坐标是(22018,22018).
故答案为:(22018,22018).


科目:初中数学 来源: 题型:
【题目】如图,数轴上![]() ,
,![]() 两点对应的数分别为
两点对应的数分别为![]() 和
和![]() ,点
,点![]() 和点
和点![]() 同时从原点出发,点
同时从原点出发,点![]() 以每秒
以每秒![]() 个单位长度的速度沿数轴正方向运动,点
个单位长度的速度沿数轴正方向运动,点![]() 以每秒
以每秒![]() 个单位长度的速度先沿数轴负方向运动,到达点
个单位长度的速度先沿数轴负方向运动,到达点![]() 后再沿数轴正方向运动,当点
后再沿数轴正方向运动,当点![]() 到达点
到达点![]() 后,两个点同时结束运动.设运动时间为
后,两个点同时结束运动.设运动时间为![]() 秒.
秒.

(1)当![]() 时,求线段
时,求线段![]() 的长度;
的长度;
(2)通过计算说明,当![]() 在不同范围内取值时,线段
在不同范围内取值时,线段![]() 的长度如何用含
的长度如何用含![]() 的式子表示?
的式子表示?
(3)当点![]() 是
是![]() 的中点时直接写出
的中点时直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC=BC=![]() ,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B,则C′B的长为( ).
,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B,则C′B的长为( ).

A. 1 B. ![]() C. 2 D.
C. 2 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂为满足市场需要,准备生产一种大型机械设备,已知生产一台这种大型机械设备需![]() ,
,![]() ,
,![]() 三种配件共
三种配件共![]() 个,且要求所需
个,且要求所需![]() 配件数量不得超过
配件数量不得超过![]() 个,
个,![]() 配件数量恰好是
配件数量恰好是![]() 配件数量的
配件数量的![]() 倍,
倍,![]() 配件数量不得低于
配件数量不得低于![]() ,
,![]() 两配件数量之和.该工厂准备生产这种大型机械设备
两配件数量之和.该工厂准备生产这种大型机械设备![]() 台,同时决定把生产
台,同时决定把生产![]() ,
,![]() ,
,![]() 三种配件的任务交给一车间.经过试验,发现一车间工人的生产能力情况是:每个工人每天可生产
三种配件的任务交给一车间.经过试验,发现一车间工人的生产能力情况是:每个工人每天可生产![]() 个
个![]() 配件或
配件或![]() 个
个![]() 配件或
配件或![]() 个
个![]() 配件.若一车间安排一批工人恰好
配件.若一车间安排一批工人恰好![]() 天能完成此次生产任务,则生产一台这种大型机械设备所需
天能完成此次生产任务,则生产一台这种大型机械设备所需![]() 配件的数量是_______个.
配件的数量是_______个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料,回答问题:
材料一:
自然数的发现是人类数学研究的开端,我们在研究自然数的时候采用的进制为十进制.现定义:位数相同且对应数位上的数字之和为10的两个数互为“亲密数”,例如:3与7互为“亲密数”,16的“亲密数”为94.
材料二:
若![]() 的“亲密数”为
的“亲密数”为![]() ,记
,记![]() 为
为![]() 的“亲密差”例如:72的“亲密数”为38.
的“亲密差”例如:72的“亲密数”为38.
![]() ,则34为72的“亲密差”.
,则34为72的“亲密差”.
根据材料,回答下列问题:
(1)请填空:64的“亲密数”为______;25的“亲密差”为______;
(2)某两位数个位上的数字比十位上的数字大2,且这个两位数的“亲密数”等于它的![]() 倍,求这个两位数的“亲密差”:
倍,求这个两位数的“亲密差”:
(3)某个三位数![]() (
(![]() ,且
,且![]() 为整数),记
为整数),记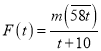 ,若
,若![]() 的值为一个整数,求这个整数
的值为一个整数,求这个整数![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,李老师和同学们做一个游戏:他在三张硬纸片上分别写出一个代数式,背面分别标上序号①、②、③,摆成如图所示的一个等式,然后翻开纸片②是4x2+5x+6,翻开纸片③是3x2﹣x﹣2.
![]()
解答下列问题
(1)求纸片①上的代数式;
(2)若x是方程2x=﹣x﹣9的解,求纸片①上代数式的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:直线y=ax+b与直线y=bx+a互为“友好直线”.如:直线y=2x+1与直线y=x+2互为“友好直线”.
(1)点M(m,2)在直线y=-x+4的“友好直线”上,则m=________;
(2)直线y=4x+3上的一点M(m,n)又是它的“友好直线”上的点,求点M的坐标;
(3)对于直线y=ax+b上的任意一点M(m,n),都有点N(2m,m-2n)在它的“友好直线”上,求直线y=ax+b的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知线段![]() 和线段
和线段![]() 外的一点
外的一点![]() ,请按下列要求画出相应的图形,并计算(不要求写画法):
,请按下列要求画出相应的图形,并计算(不要求写画法):
(1)①延长线段![]() 到
到![]() ,使
,使![]() ;
;
②若![]() ,点
,点![]() 是直线
是直线![]() 上一点,且
上一点,且![]() ,求线段
,求线段![]() 的长.
的长.
(2)过点![]() 画
画![]() 于点
于点![]() ,连结
,连结![]() 、
、![]() 并用直尺测量线段
并用直尺测量线段![]() 、
、![]() 、
、![]() 的长,并指出哪条线段可以表示点
的长,并指出哪条线段可以表示点![]() 到线段
到线段![]() 的距离.(测量数据直接标注在图形上,结果精确到
的距离.(测量数据直接标注在图形上,结果精确到![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
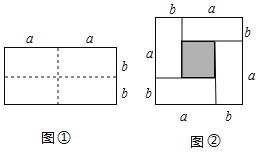
【题目】(1)如图①是一个长为2a,宽为2b的长方形,若将此图中虚线用剪刀均分为四块小长方形,然后按图②的形状拼成一个正方形,请问:这两个图形的什么量不变?请填写这个量的名称 .所得的正方形的面积比原长方形的面积多出的阴影部分的面积用含a,b的代数式表示 ;
(2)由①的探索中,可以得出的结论是:在周长一定的长方形中,当 时,面积最大;
(3)若一长方形的周长为36厘米,则当边长为多少时,该图形的面积最大?最大面积是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com