
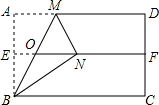 如图,对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展平,再一次折叠纸片,使点A落在EF上的点N处,折痕过定点B,得到折痕MB,MB与EF交于点O,则△MON是( )
如图,对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展平,再一次折叠纸片,使点A落在EF上的点N处,折痕过定点B,得到折痕MB,MB与EF交于点O,则△MON是( )| A. | 正三角形 | B. | 直角三角形 | C. | 等腰三角形 | D. | 等腰直角三角形 |
分析 延长MN,MN的延长线于BC相交于点G.由平行线分线段成比例定理可知:MN=NG,由翻折的性质可知BN⊥MG,从而可证明∠BMG=∠BGM,由结合平行线的性质可证明∠BMG=∠MNO,然后再证明∠MON=∠OMN,从而可到∠MON=∠OMN=∠MN0.
解答 解:如图所示,延长MN,MN的延长线于BC相交于点G.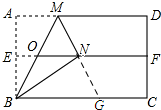
∵AD与BC重合,得到折痕EF
∴EF‖AD‖BC 且AE=EB.
∴MN=NG.
由折叠的性质可知;∠MNB=∠A=90°,∠AMO=∠OMN.
∵MN=GN,BN⊥MG,
∴BM=BG.
∴∠BMG=∠BGM.
∵EN∥BG,
∴∠MNE=∠BGM.
∴∠BMG=∠MNO.
∵AD∥EF,
∴∠MAO=∠MON.
∴∠MON=∠OMN.
∴∠MON=∠OMN=∠MN0.
∴△MNO为等边三角形.
故选:A.
点评 本题主要考查的是平行线分线段成比例定理、翻折的性质、线段垂直平分线的性质、等边三角形的判定,证得∠BMG=∠MNO,∠MON=∠OMN是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
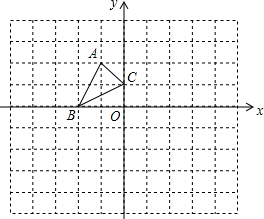 △ABC平面在直角坐标系中的位置如图所示(其中每个小正方形的边长均为1),点A(-1,2),点B(-2,0),点C(0,1).
△ABC平面在直角坐标系中的位置如图所示(其中每个小正方形的边长均为1),点A(-1,2),点B(-2,0),点C(0,1).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com