
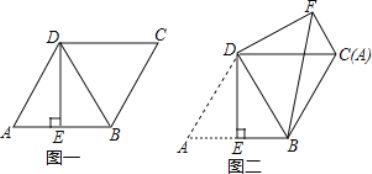
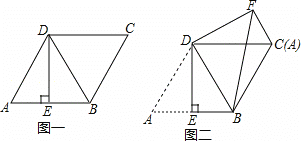
【题目】如图一,菱形ABCD的边长为2,点E是AB的中点,且DE⊥AB.
(1)求证:△ABD是等边三角形;
(2)将图一中△ADE绕点D逆时针旋转,使得点A和点C重合,得到△CDF,连接BF,如图二,求线段BF的长.
【答案】(1)证明见解析;(2)![]()
【解析】(1)利用线段垂直平分线的性质得出AD=BD,进而利用菱形的性质得出AD=AB,即可得出△ABD是等边三角形;
(2)利用旋转的性质以及平行线的性质得出∠FDB=90°,再结合勾股定理得出BF的长.
(1)证明:如图一,
∵点E是AB的中点,且DE⊥AB,
∴AD=BD,
∵四边形ABCD是菱形,
∴AD=AB,
∴AD=DB=AB,
∴△ABD是等边三角形;
(2)解:如图二,
由(1)得:△ABD是等边三角形,则∠ADE=∠BDE,
∵四边形ABCD是菱形,
∴AB∥DC,
∵DE⊥AB,
∴∠EDC=90°,
∴∠BDF=∠FDC+∠CDB=∠EDB+∠CDB=90°,
∵△ADE绕点D逆时针旋转,使得点A和点C重合,得到△CDF,
∴DF=ED=![]() ,BD=2,
,BD=2,
∴BF=![]() .
.
“点睛”此题主要考查了勾股定理以及旋转的性质和等边三角形的判定、菱形的性质等知识,熟练利用已知得出AD=BD是解题关键.


科目:初中数学 来源: 题型:
【题目】京沈高速铁路赤峰至喀左段正在建设中,甲、乙两个工程队计划参与一项工程建设,甲队单独施工30天完成该项工程的![]() ,这时乙队加入,两队还需同时施工15天,才能完成该项工程.
,这时乙队加入,两队还需同时施工15天,才能完成该项工程.
(1)若乙队单独施工,需要多少天才能完成该项工程?
(2)若甲队参与该项工程施工的时间不超过36天,则乙队至少施工多少天才能完成该项工程?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知三角形的三个顶点坐标分别是(-1,4)、(1,1)、(-4,-1),现将这三个点先向右平移2个单位长度,再向上平移3个单位长度,则平移后三个顶点的坐标是( )
A. (-2,2),(3,4),(1,7) B. (-2,2),(4,3),(1,7)
C. (2,2),(3,4),(1,7) D. (2,-2),(3,3),(1,7)
查看答案和解析>>
科目:初中数学 来源: 题型:
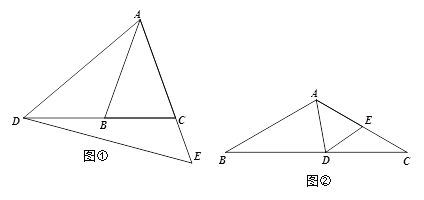
【题目】如图,△ABC中,![]() ,点D在BC所在的直线上,点E在射线AC上,且
,点D在BC所在的直线上,点E在射线AC上,且![]() ,连接DE.
,连接DE.
(1)如图①,若![]() ,
,![]() ,求
,求![]() 的度数;
的度数;
(2)如图②,若![]() ,
,![]() ,求
,求![]() 的度数;
的度数;
(3)当点D在直线BC上(不与点B、C重合)运动时,试探究![]() 与
与![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各式中,计算结果是x2+7x -18的是( )
A.(x-1)(x+18)
B.(x+2)(x+9)
C.(x-3)(x+6)
D.(x-2)(x+9)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在电影票上,将7排6号“简记作(7,6)”
(1)6排7号可表示为___________;(2) (8,6)表示的意义是______________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com