
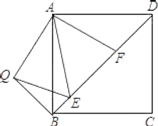
【题目】如图,在正方形ABCD中,E,F是对角线B上两点,且∠EAF=45°,将△ADF绕点A顺时针旋转90°后得到△ABQ,连接EQ,
求证:(1)EA是∠QAF的平分线;
(2)BD=BE+QE+QB.
【答案】(1)见解析;(2)见解析
【解析】
(1)由旋转的性质可知∠QAF=90°,再证明∠EAF=∠EAQ=45°即可说明EA是∠QAF的平分线;
(2)先证明△QAE≌△FAE得到QE=EF,则BD=BE+EF+FD=BE+QE+QB.
解:证明:(1)由旋转的性质可知∠QAF=90°,
∵∠EAF=45°,
∴∠EAQ=∠QAF﹣∠EAF=90°﹣45°=45°.
∴∠EAF=∠EAQ.
∴EA是∠QAF的平分线;
(2)由旋转的性质可知AQ=AF,QB=FD,
由(1)可知∠EAQ=∠EAF=45°,
又AE=AE,
∴△QAE≌△FAE(SAS).
∴QE=EF.
∴BD=BE+EF+FD=BE+QE+QB.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,∠AOB=45°,点M,N在边OA上,OM=x,ON=x+4,点P是边OB上的点.若使点P,M,N构成等腰三角形的点P恰好有三个,则x的值是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,割线PCD交⊙O于C、D,∠PAE=∠PDA.
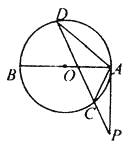
(1)求证:PA是⊙O的切线;
(2)若PA=6,CD=3PC,求PD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
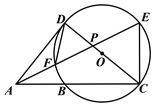
【题目】如图,△ACE,△ACD均为直角三角形,∠ACE=90°,∠ADC=90°,AE与CD相交于点P,以CD为直径的⊙O恰好经过点E,并与AC,AE分别交于点B和点F.
(1)求证:∠ADF=∠EAC.
(2)若PC=![]() PA,PF=1,求AF的长.
PA,PF=1,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】函数y=ax2+bx+c的图象如图所示,那么关于x的一元二次方程ax2+bx+c-3=0的根的情况是( )
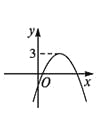
A. 有两个不相等的实数根
B. 有两个异号的实数根
C. 有两个相等的实数根
D. 没有实数根
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个涵洞的截面边缘是抛物线形.现测得当水面宽AB=1.6m时,涵洞顶点与水面的距离是2.4m.这时,离开水面1.5m处,涵洞的宽DE为_____.
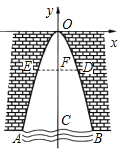
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点E是边AD上一点,过点E作EF⊥BC,垂足为点F,将△BEF绕着点E逆时针旋转,使点B落在边BC上的点N处,点F落在边DC上的点M处,若点M恰好是边CD的中点,那么![]() 的值是( )
的值是( )
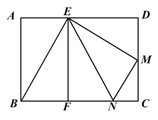
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
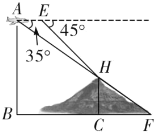
【题目】如图所示,为了测量某矿山CH的高度,科考组在距离矿山一段距离的B点乘坐直升机垂直上升2000米至A点,在A点,在A点观察H点的俯角为![]() ,然后乘坐直升机从A水平向前飞行500米到E点,此时观察H点的俯角为
,然后乘坐直升机从A水平向前飞行500米到E点,此时观察H点的俯角为![]() ,所有的点都在同一平面内,科考队至此完成了数据监测,请你依据数据计算科考队测得的矿山高度.(结果保留整数,参考数据:
,所有的点都在同一平面内,科考队至此完成了数据监测,请你依据数据计算科考队测得的矿山高度.(结果保留整数,参考数据:![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com