
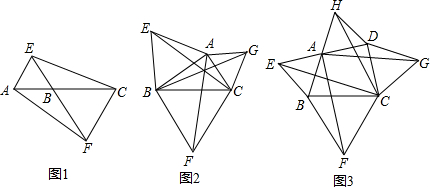
���� ��1�����ݵȱ������ε����ʺ�ȫ�������ε��ж�����֤����AEC�ա�AEF���ɣ�
��2��֤����ACF�ա�GCB���ɣ�
��3��֤����EBC�ա�ABF���ɵõ��𰸣�
��� �⣺��1��AF=CE���ߡ�ABE����BCF�ǵȱ������Σ�
���AEB=��EAB=60�㣬AB=BE��BC=BF��
��AC=EF��
�ڡ�AEC���AFE�У�
$\left\{\begin{array}{l}{AE=AE}\\{��AEB=��EAB}\\{AC=EF}\end{array}\right.$��
���AEC�ա�AEF��
��AF=CE��
�ʴ�Ϊ����ȣ�
��2��AF=BG=EC��
�ߡ�BCF����ACG�ǵȱ������Σ�
��AC=GC��FC=BC����BCF=��ACG=60�㣬
���BCF+��ACB=��ACG+��ACB������ACF=��GCB��
�ڡ�ACF���GCB��
$\left\{\begin{array}{l}{AC=GC}\\{��ACF=��GCB}\\{FC=BC}\end{array}\right.$��
���ACF�ա�GCB��
��AF=BG��ͬ��EC=BG��
��AF=BG=EC��
��3���ߡ�AEB����BCF�ǵȱ������Σ�
��BE=BA��BC=BF����ABE=��CBF=60�㣬
���ABE+��ABC=��CBF+��ABC������EBC=��ABF��
�ڡ�EBC���ABF�У�
$\left\{\begin{array}{l}{BE=BA}\\{��EBC=��ABF}\\{BC=BF}\end{array}\right.$��
���EBC�ա�ABF��
��AF=EC��
ͬ��AF=EC=AG=HC��
�ʴ�Ϊ��AF=EC=AG=HC��
���� ���⿼�����ȫ�������ε��ж��������Լ��ȱ������ε����ʣ�����ȫ�������ε��ж����������ʶ����Լ��ȱ������ε������Ƕ���60�㡢����������ǽ���Ĺؼ���


 ����������������ϵ�д�
����������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
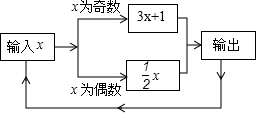 ��һ����ֵת������ԭ����ͼ��ʾ������ʼ����x��ֵ��3���ɷ��ֵ�1������Ľ����10����2������Ľ����5����3������Ľ����16�����μ�����ȥ������101������Ľ����4��
��һ����ֵת������ԭ����ͼ��ʾ������ʼ����x��ֵ��3���ɷ��ֵ�1������Ľ����10����2������Ľ����5����3������Ľ����16�����μ�����ȥ������101������Ľ����4���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
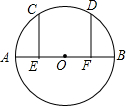 ��ͼ��AB�ǡ�O��ֱ������E��F�ֱ���OA��OB���е㣬��EC��AB��FD��AB��EC��FD����O��C��D���㣬��֤��$\widehat{AC}$=$\widehat{BD}$��
��ͼ��AB�ǡ�O��ֱ������E��F�ֱ���OA��OB���е㣬��EC��AB��FD��AB��EC��FD����O��C��D���㣬��֤��$\widehat{AC}$=$\widehat{BD}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
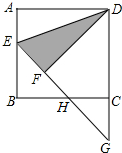 ��ͼ����E��������ABCD�ı�AB��һ�㣬�ҡ�ADE=22.5�㣬����ADE��DE���۵õ���FDE���ӳ�EF��BC�ڵ�H����DC���ӳ����ڵ�G����ͼ�����еĵ����������ǡ�EBH����GHC����EDG������������������������ȫ���оٳ�������
��ͼ����E��������ABCD�ı�AB��һ�㣬�ҡ�ADE=22.5�㣬����ADE��DE���۵õ���FDE���ӳ�EF��BC�ڵ�H����DC���ӳ����ڵ�G����ͼ�����еĵ����������ǡ�EBH����GHC����EDG������������������������ȫ���оٳ��������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com