
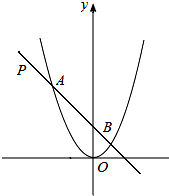
 如图,若点P的坐标为(-2,2),过点P的一条直线交抛物线y=x2于A、B两点,当PA=AB时,点A的坐标是(-1,1)或(-3,9).
如图,若点P的坐标为(-2,2),过点P的一条直线交抛物线y=x2于A、B两点,当PA=AB时,点A的坐标是(-1,1)或(-3,9). 分析 设A(m,m2),分别过点P、A、B作x轴垂线,垂足分别为点G、E、F,用m表示出OF和BF的长,根据点B在抛物线y=x2上,即可求出点A的坐标.
解答 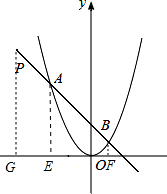 解:设A(m,m2),
解:设A(m,m2),
如图所示,分别过点P、A、B作x轴垂线,垂足分别为点G、E、F.
∵PA=AB,
∴AE是梯形PGFB的中位线,
∴GE=EF,AE=$\frac{1}{2}$(PG+BF).
∵OF=|EF-OE|,GE=EF,
∴OF=|GE-EO|,
∵GE=GO-EO=2+m,EO=-m,
∴OF=|2+m-(-m)|=|2+2m|,
∴OF=2m+2,
∵AE=$\frac{1}{2}$(PG+BF),
∴BF=2AE-PG=2m2-2,
∴B(2+2m,2m2-2).
∵点B在抛物线y=x2上,
∴2m2-2=(2+2m)2
解得:m=1或-3,
当m=-1时,m2=1;当m=-3时,m2=9,
点A的坐标为(-1,1)或(-3,9).
故答案为(-1,1)或(-3,9).
点评 本题主要考查了二次函数的性质,解答本题的关键是正确地作出辅助线,求出点B的坐标,此题有一定的难度.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | t>27 | B. | t≤20 | C. | 20<t<27 | D. | 20≤t≤27 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (3,8) | B. | (4,7) | C. | (5,6) | D. | (6,5) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 不变 | B. | 减少9平方厘米 | C. | 增加9平方厘米 | D. | 不能确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com