
【题目】如图,在直角坐标系中,△ABC的三个顶点都在坐标轴上,A,B两点关于y轴对称,点C是y轴正半轴上一个动点,AD是角平分线.
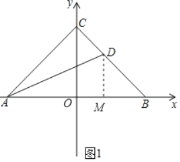
(1)如图1,若∠ACB=90°,直接写出线段AB,CD,AC之间数量关系;
(2)如图2,若AB=AC+BD,求∠ACB的度数;
(3)如图2,若∠ACB=100°,求证:AB=AD+CD.

【答案】(1)AB=AC+CD;(2)108°;(3)证明见解析
【解析】
(1)如图1,过D作DM⊥AB于M,根据轴对称的性质得到CA=CB,根据角平分线的性质得到CD=MD,∠ABC=45°,根据全等三角形的性质得到AC=AM,于是得到结论;
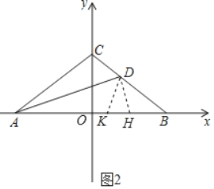
(2)设∠ACB=α,则∠CAB=∠CBA=90°-![]() α,在AB上截取AK=AC,连结DK,根据角平分线的定义得到∠CAD=∠KAD,根据全等三角形的性质得到∠ACD=∠AKD=α,根据三角形的内角和即可得到结论;
α,在AB上截取AK=AC,连结DK,根据角平分线的定义得到∠CAD=∠KAD,根据全等三角形的性质得到∠ACD=∠AKD=α,根据三角形的内角和即可得到结论;
(3)如图2,在AB上截取AH=AD,连接DH,根据等腰三角形的性质得到∠CAB=∠CBA=40°,根据角平分线的定义得到∠HAD=∠CAD=20°,求得∠ADH=∠AHD=80°,在AB上截取AK=AC,连接DK,根据全等三角形的性质得到∠ACB=∠AKD=100°,CD=DK,根据等腰三角形的性质得到DH=BH,于是得到结论.
(1)如图1,过D作DM⊥AB于M,
∵A,B两点关于y轴对称,
∴CA=CB,
∵∠ACB=90°,AD是角平分线,
∴CD=MD,∠ABC=45°,
∴∠BDM=45°,
∴BM=DM,
∴BM=CD,
在RT△ADC和RT△ADM中,![]() ,
,
∴RT△ADC≌RT△ADM(HL),
∴AC=AM,
∴AB=AM+BM=AC+CD,
即AB=AC+CD;
(2)设∠ACB=α,则∠CAB=∠CBA=90°﹣![]() α,
α,
在AB上截取AK=AC,连结DK,
∵AB=AC+BD,
∴BK=BD,
∵AD是角平分线,
∴在△CAD和△KAD中,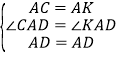 ,
,
∴△CAD≌△KAD(SAS),
∴∠ACD=∠AKD=α,
∴∠BKD=180°﹣α,
∵BK=BD,
∴∠BDK=180°﹣α,
在△BDK中,
180°﹣α+180°﹣α+90°﹣![]() α=180°,
α=180°,
∴α=108°,
∴∠ACB=108°;
(3)如图2,在AB上截取AH=AD,连接DH,
∵∠ACB=100°,AC=BC,
∴∠CAB=∠CBA=40°,
∵AD是角平分线,
∴∠HAD=∠CAD=20°,
∴∠ADH=∠AHD=80°,
在AB上截取AK=AC,连接DK,
由(1)得,△CAD≌△KAD,
∴∠ACB=∠AKD=100°,CD=DK,
∴∠DKH=80°=∠DHK,
∴DK=DH=CD,
∵∠CBA=40°,
∴∠BDH=40°,
∴DH=BH,
∴BH=CD,
∵AB=AH+BH,
∴AB=AD+CD.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】有一张边长为![]() 厘米的正方形桌面,因为实际需要,需将正方形边长增加
厘米的正方形桌面,因为实际需要,需将正方形边长增加![]() 厘米,木工师傅设计了如图所示的三种方案:
厘米,木工师傅设计了如图所示的三种方案:

小明发现这三种方案都能验证公式:![]() .
.
对于方案一,小明是这样验证的:
![]() 大正方形面积可表示为:
大正方形面积可表示为:![]() ,也可以表示为:
,也可以表示为:![]() ,
,
![]() .
.
请你仿照上述方法根据方案二、方案三,写出公式的验证过程.
(1)方案二:
(2)方案三:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如果两个三角形两边和其中一边所对的角相等,则两个三角形全等,这是一个假命题,请画图举例说明;
(2)如图,在△ABC和△DEF中,AB=ED,BC=DF,∠BAC=∠DEF=120°,求证:△ABC≌△EDF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,其中A点坐标为(﹣1,0),点C(0,5),另抛物线经过点(1,8),M为它的顶点.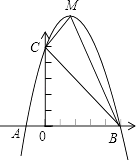
(1)求抛物线的解析式;
(2)求△MCB的面积S△MCB .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com