
【题目】综合探究:
(1)如图1,AB是⊙O的直径,点C、D在上, ![]() .若AB=13,BC=12,直接写出CD的长;
.若AB=13,BC=12,直接写出CD的长;
(2)如图2,AB、CD是⊙O的两条互相垂直的直径,E是劣弧AD上一点,AE的延长线交CD的延长线于F,过O作OG∥AE交CE于G,求AE:CG的值;
(3)如图3,∠ACB=90°,AC=BC,点P为AB的中点.若点E满足AE=![]() AC,CE=CA,点Q为AE的中点,则
AC,CE=CA,点Q为AE的中点,则![]() = .
= .
【答案】(1)CD=![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1) 连接AC、BD,可得AD=BD,再利用E、A、C三点共线,勾股定理即可解答.
(2) 作OH⊥OG,交CE于H,连接AH,证明△COG≌△AOH即可解答.
(3) 分点E在直线AC的左侧和右侧两种情况进行讨论, 利用勾股定理即可解答.
解:(1)如图1,连接AC、BD,
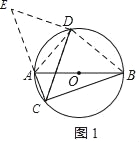
∵AB是⊙O的直径,
∴∠ADB=∠ACB=90°,
∵![]() =
=![]() ,
,
∴AD=BD,
将△BCD绕点D,逆时针旋转90°到△AED处,
∴∠EAD=∠DBC,
∵∠DBC+∠DAC=180°,
∴∠EAD+∠DAC=180°,
∴E、A、C三点共线,
∵AB=13,BC=12,
∴由勾股定理可求得:AC=5,
∵BC=AE,
∴CE=AE+AC=17,
∵∠EDA=∠CDB,
∴∠EDA+∠ADC=∠CDB+∠ADC,即∠EDC=∠ADB=90°,
∵CD=ED,
∴△EDC是等腰直角三角形,
∴CE=![]() CD,
CD,
∴CD=![]() ;
;
(2)作OH⊥OG,交CE于H,连接AH,
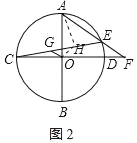
∵OG∥AE,
∴∠OGH=∠AEC=45°,
∴∠OHG=45°,
∴OG=OH,
又∵∠COG=∠AOH=90°﹣∠AOG,OC=OA,
∴△COG≌△AOH(SAS),
∴CG=AH,∠AHO=∠CGO=135°,
∴∠AHC=90°,
∴AE=![]() AH=
AH=![]() CG,
CG,
∴![]() =
=![]() .
.
(3)如图3,当点E在直线AC的左侧时,连接CQ,PC,
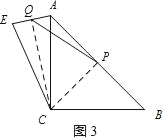
∵AC=BC,∠ACB=90°,
点P是AB的中点,
∴AP=CP,∠APC=90°,
又∵CA=CE,点Q是AE的中点,
∴∠CQA=90°,
设AC=a,
∵AE=![]() AC,
AC,
∴AE=![]() a,
a,
∴AQ=![]() AE=
AE=![]() a,
a,
由勾股定理可求得:CQ=![]() a,
a,
∵AQ+CQ=![]() PQ,
PQ,
∴![]() PQ=
PQ=![]() a+
a+![]() a,
a,
∴![]() PQ=
PQ=![]() AC,即
AC,即![]() =
=![]() ;
;
如图4,当点E在直线AC的右侧时,连接CQ、CP,
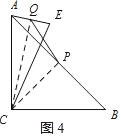
同理可知:∠AQC=∠APC=90°,
设AC=a,
∴AQ=![]() AE=
AE=![]() a,
a,
由勾股定理可求得:CQ=![]() a,
a,
又PQ=![]() (CQ﹣AQ),
(CQ﹣AQ),
∴![]() PQ=
PQ=![]() AC,即
AC,即![]() =
=![]() ;
;
综上,![]() =
=![]() ,
,
故答案为:![]() .
.


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:
【题目】定义:
我们知道,四边形的一条对角线把这个四边形分成了两个三角形,如果这两个三角形相似(不全等),我们就把这条对角线叫做这个四边形的“相似对角线”.
理解:
(1)如图1,已知Rt△ABC在正方形网格中,请你只用无刻度的直尺在网格中找到一点D,使四边形ABCD是以AC为“相似对角线”的四边形(保留画图痕迹,找出3个即可);
(2)如图2,在四边形ABCD中,∠ABC=80°,∠ADC=140°,对角线BD平分∠ABC.
求证:BD是四边形ABCD的“相似对角线”;
(3)如图3,已知FH是四边形EFCH的“相似对角线”,∠EFH=∠HFG=30°,连接EG,若△EFG的面积为2![]() ,求FH的长.
,求FH的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,点E为边AD的中点,且∠ABC=60°,AB=6,BE交AC于点F,则AF=( )
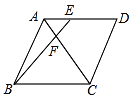
A. 1 B. 2 C. 2.5 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上.将△ABC绕点A顺时针旋转90°得到△AB1C1.
(1)在网格中画出△AB1C1;
(2)计算点B旋转到B1的过程中所经过的路径长.(结果保留π)

查看答案和解析>>
科目:初中数学 来源: 题型:
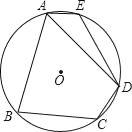
【题目】如图,在⊙O的内接四边形ABCD中,AB=AD,∠C=120°,点E在![]() 上.
上.
(1)求∠E的度数;
(2)连接OD、OE,当∠DOE=90°时,AE恰好为⊙O的内接正n边形的一边,求n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
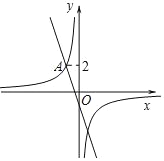
【题目】如图,在平面直角坐标系xOy中,直线y=kx+m与双曲线y=﹣![]() 相交于点A(m,2).
相交于点A(m,2).
(1)求直线y=kx+m的表达式;
(2)直线y=kx+m与双曲线y=﹣![]() 的另一个交点为B,点P为x轴上一点,若AB=BP,直接写出P点坐标.
的另一个交点为B,点P为x轴上一点,若AB=BP,直接写出P点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
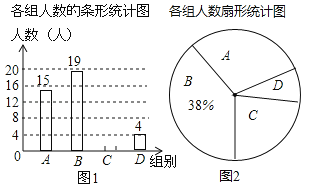
【题目】小明随机调查了若干市民租用共享单车的骑车时间t(单位:分),将获得的数据分成四组,绘制了如下统计图(A:0<t≤10,B:10<t≤20,C:20<t≤30,D:t>30),根据图中信息,解答下列问题:
(1)这项被调查的总人数是多少人?
(2)试求表示A组的扇形统计图的圆心角的度数,补全条形统计图;
(3)如果小明想从D组的甲、乙、丙、丁四人中随机选择两人了解平时租用共享单车情况,请用列表或画树状图的方法求出恰好选中甲的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在小山的东侧A点有一个热气球,由于受风的影响,以30米/分的速度沿与地面成75°角的方向飞行,25分钟后到达C处,此时热气球上的人测得小山西侧B点的俯角为30°,则小山东西两侧A,B两点间的距离为( )米.

A. 750![]() B. 375
B. 375![]() C. 375
C. 375![]() D. 750
D. 750![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com