
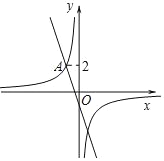
【题目】如图,在平面直角坐标系xOy中,直线y=kx+m与双曲线y=﹣![]() 相交于点A(m,2).
相交于点A(m,2).
(1)求直线y=kx+m的表达式;
(2)直线y=kx+m与双曲线y=﹣![]() 的另一个交点为B,点P为x轴上一点,若AB=BP,直接写出P点坐标.
的另一个交点为B,点P为x轴上一点,若AB=BP,直接写出P点坐标.
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,过⊙O外一点P作⊙O的两条切线PC,PD,切点分别为C,D,连接OP,CD.
(1)求证:OP⊥CD;
(2)连接AD,BC,若∠DAB=50°,∠CBA=70°,OA=2,求OP的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中正确的是( )
A. “打开电视机,正在播《动物世界》”是随机事件
B. 某种彩票的中奖概率为千分之一,说明每买1000张彩票,一定有一张中奖
C. 抛掷一枚质地均匀的硬币一次,出现正面朝上的概率为三分之一
D. 任意画一个三角形,其内角和为360°是必然事件
查看答案和解析>>
科目:初中数学 来源: 题型:
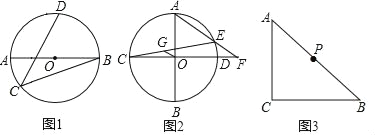
【题目】综合探究:
(1)如图1,AB是⊙O的直径,点C、D在上, ![]() .若AB=13,BC=12,直接写出CD的长;
.若AB=13,BC=12,直接写出CD的长;
(2)如图2,AB、CD是⊙O的两条互相垂直的直径,E是劣弧AD上一点,AE的延长线交CD的延长线于F,过O作OG∥AE交CE于G,求AE:CG的值;
(3)如图3,∠ACB=90°,AC=BC,点P为AB的中点.若点E满足AE=![]() AC,CE=CA,点Q为AE的中点,则
AC,CE=CA,点Q为AE的中点,则![]() = .
= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】函数y=ax2+bx+c的图像如图所示,那么关于x的方程ax2+bx+c-4=0的根的情况是( )

A.有两个不相等的实数根 B.有两个异号的实数根
C.有两个相等的实数根 D.没有实数根
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0),B(3,0),与y轴交于点C.过点C作CD∥x轴,交抛物线的对称轴于点D.
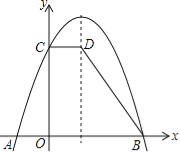
(1)求该抛物线的解析式;
(2)若将该抛物线向下平移m个单位,使其顶点落在D点,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,点P在对角线AC上,且PA=PD,⊙O是△PAD的外接圆.
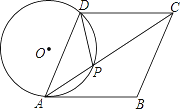
(1)求证:AB是⊙O的切线;
(2)若AC=8,tan∠BAC=![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读以下材料,并解决相应问题:
材料一:换元法是数学中的重要方法,利用换元法可以从形式上简化式子,在求解某些特殊方程时,利用换元法常常可以达到转化的目的,例如在求解一元四次方程![]() ,就可以令
,就可以令![]() ,则原方程就被换元成
,则原方程就被换元成![]() ,解得 t 1,即
,解得 t 1,即![]() ,从而得到原方程的解是 x 1
,从而得到原方程的解是 x 1
材料二:杨辉三角形是中国数学上一个伟大成就,在中国南宋数学家杨辉 1261 年所著的《详解九章算法》一书中出现,它呈现了某些特定系数在三角形中的一种有规律的几何排列,下图为杨辉三角形:

……………………………………
(1)利用换元法解方程:![]()
(2)在杨辉三角形中,按照自上而下、从左往右的顺序观察, an 表示第 n 行第 2 个数(其中 n≥4),bn 表示第 n 行第 3 个数,![]() 表示第
表示第![]() 行第 3 个数,请用换元法因式分解:
行第 3 个数,请用换元法因式分解:![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com