Question

16．阅读：已知如图（1）△ABC中，AB=AC，CF为AB边上的高，P为BC边上的一个动点，PD⊥AB，PE⊥AC，探究PD、PE和CF之间的关系．聪明的小强连接AP通过S_△APB+S_△APC=S_△ABC，从而发现PD+PE=CF．
理解：小强对上述问题进一步进行探究，当点P在BC延长线上时，如图2，其它条件不变，发现PD-PE=CF，请你证明小强的这一发现．
运用（一）：如图3，将矩形ABCD沿EF折叠，使点D落在点B上，点C落在点C′处，P为折痕EF上的任意一点，PG⊥BE，PH⊥BC，若AD=8，CF=3，求PG+PH的值．
运用（二）：如图4，四边形ABCD中，E为AD边上的点，且EB⊥AB，CE⊥CD，且AB•CE=CD•BE，M、N分别为AE、DE的中点，若AD=10，sinA=$\frac{3}{5}$，求△BEM与△CEN的周长之和．

Answer 1

分析 运用（一）：先依据矩形的性质和翻折的性质证明∠BEF=∠BFE，从而得到△EBF为等腰三角形，依据例题结论可知PG+PH=BC′，然后再在Rt△BFC′中依据勾股定理求得FC′的长即可；
运用（二）：先证明△ABE∽△DCE，从而可求得∠D=∠A，由锐角三角函数的定义以及相似三角形的对应中线的比等于相似比可求得MB+CN=$\frac{3}{5}$AD，然后由直角三角形斜边上中线的性质可知MA=BM，CN=ND，从而可求得△BEM与△CEN的周长之和．

解答 解：运用（一）：过点F作FM⊥BE，垂足为M．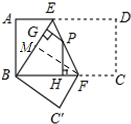

∵AD∥BC，
∴∠BFE=∠DEF．
由翻折的性质可知：∠DEF=∠BEF．
∴∠BEF=∠BFE．
∴BE=BF．
由例题结论可知GP+HP=MF．
∵∠EBC′=∠EMF=90°，
∴MF∥BC′．
∵BE∥C′F，MF∥BC′，
∴BC′=MF．
∵FC′=FC=3，BC=AD=8，
∴BF=5．
∵在Rt△BFC′中，BC′=$\sqrt{B{F}^{2}-FC{′}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4．
∴GP+HP=4．
运用（二）：∵EB⊥AB，CE⊥CD，
∴∠ABE=∠DCE．
∵AB•CE=CD•BE，
∴$\frac{AB}{CD}=\frac{BE}{EC}$．
∴△ABE∽△DCE．
∴∠D=∠A．
∴BE=$\frac{3}{5}$AE，EC=$\frac{3}{5}$DE．
∴BE+EC=$\frac{3}{5}$AD=$\frac{3}{5}$×10=6．
∵在Rt△AEB中，M是AE的中点，
∴BM=AM=ME．
∴ME+BM=AE．
同理：EN+NC=ED．
∴△BEM与△CEN的周长之和=BE+BM+ME+NC+EN+EC=（BE+CE）+（AE+DE）=6+10=16．

点评 本题主要考查的是四边形的综合应用，解答本题主要应用了矩形的性质、翻折的性质、勾股定理、等腰三角形的性质和判定、相似三角形的性质和判定，直角三角形斜边上中线的性质，证得三角形BEF为等腰三角形是解答应用（一）的关键，找出△BEM与△CEN的周长之和与AD的长度的关系是解答应用（二）的关键．