为弘扬“东亚文化”，某单位开展了“东亚文化之都”演讲比赛，在安排1位女选手和3位男选手的出场顺序时，采用随机抽签方式．
（1）请直接写出第一位出场是女选手的概率；
（2）请你用画树状图或列表的方法表示第一、二位出场选手的所有等可能结果，并求出他们都是男选手的概率．
科目：初中数学 来源： 题型：
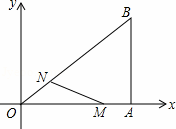
如图，在直角坐标系中，Rt△OAB的直角顶点A在x轴上，OA=4，AB=3．动点M从点A出发，以每
秒1个单位长度的速度，沿AO向终点O移动；同时点N从点O出发，以每秒1.25个单位长度的速度，沿OB向终点B移动．当两个动点运动了x秒（0＜x＜4）时，解答下列问题：
（1）求点N的坐标（用含x的代数式表示）；
（2）设△OMN的面积是S，求S与x之间的函数表达式；当x为何值时，S有最大值？最大值是多少
？
（3）在两个动点运动过程中，是否存在某一时刻，使△OMN是直角三角形？若存在，求出x的值；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
阅读理解
抛物线y=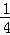
x2上任意一点到点（0，1）的距离与到直线y=﹣1的距离相等，你可以利用这一性质解决问题．
问题解决
如图，在平面直角坐标系中，直线y=kx+1与y轴交于C点，与函数y=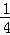x2的图象交于A，B两点，分别过A，B两点作直线y=﹣1的垂线，交于E，F两点．
（1）写出点C的坐标，并说明∠ECF=90°；
（2）在△PEF中，M为EF中点，P为动点．
①求证：PE2+PF2=2（PM2+EM2）；
②已知PE=PF=3，以EF为一条对角线作平行四边形CEDF，若1＜PD＜2，试求CP的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
荆州素有“鱼米之乡”的美称，某渔业公司组织20辆汽车装运鲢鱼、草鱼、青鱼共120吨去外地销售，按计划20辆汽车都要装运，每辆汽车只能装运同一种鱼，且必须装满，根据下表提供的信息，解答以下问题：
| 鲢鱼 | 草鱼 | 青鱼 | |
| 每辆汽车载鱼量（吨） | 8 | 6 | 5 |
| 每吨鱼获利（万元） | 0.25 | 0.3 | 0.2 |
（1）设装运鲢鱼的车辆为x辆，装运草鱼的车辆为y辆，求y与x之间的函数关系式；
（2）如果装运每种鱼的车辆都不少于2辆，那么怎样安排车辆能使此次销售获利最大？并求出最大利润．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
；
=
．
表示的平面区域的面积为
，则实数
的值为
B．
D．
中，
的值是（ ）