
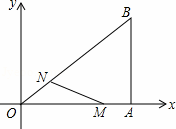
如图,在直角坐标系中,Rt△OAB的直角顶点A在x轴上,OA=4,AB=3.动点M从点A出发,以每 秒1个单位长度的速度,沿AO向终点O移动;同时点N从点O出发,以每秒1.25个单位长度的速度,沿OB向终点B移动.当两个动点运动了x秒(0<x<4)时,解答下列问题:
秒1个单位长度的速度,沿AO向终点O移动;同时点N从点O出发,以每秒1.25个单位长度的速度,沿OB向终点B移动.当两个动点运动了x秒(0<x<4)时,解答下列问题:
(1)求点N的坐标(用含x的代数式表示);
(2)设△OMN的面积是S,求S与x之间的函数表达式;当x为何值时,S有最大值?最大值是多少 ?
?
(3)在两个动点运动过程中,是否存在某一时刻,使△OMN是直角三角形?若存在,求出x的值;若不存在,请说明理由.
解:(1)根据题意得:MA=x,ON=1.25x,
在Rt△OAB中,由勾股定理得:OB=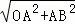 =
=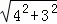 =5,
=5,
作NP⊥OA于P,如图1所示:
则NP∥AB,
∴△OPN∽△OAB,
∴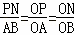 ,
,
即 ,
,
解得:OP=x,PN=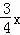 ,
,
∴点N的坐标是(x,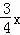 );
);
(2)在△OMN中,OM=4﹣x,OM边上的高PN=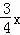 ,
,
∴S=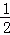 OM•PN=
OM•PN=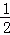 (4﹣x)•
(4﹣x)•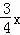 =﹣
=﹣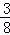 x2+
x2+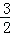 x,
x,
∴S与x之间的函数表达式为S=﹣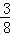 x2+
x2+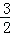 x(0<x<4),
x(0<x<4),
配方得:S=﹣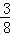 (x﹣2)2+
(x﹣2)2+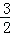 ,
,
∵﹣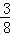 <0,
<0,
∴S有最大值,
当x=2时,S有最大值,最大值是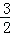 ;
;
(3)存在某一时刻,使△OMN是直角三角形,理由如下:
分两种情况:①若∠OMN=90°,如图2所示:
则MN∥AB,
此时OM=4﹣x,ON=1.25x,
∵MN∥AB,
∴△OMN∽△OAB,
∴ ,
,
即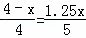 ,
,
解得:x=2;
②若∠ONM=90°,如图3所示:
则∠ONM=∠OAB,
此时OM=4﹣x,ON=1.25x,
∵∠ONM=∠OAB,∠MON=∠BOA,
∴△OMN∽△OBA,
∴ ,
,
即 ,
,
解得:x= ;
;
综上所述:x的值是2秒或 秒.
秒.





 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:初中数学 来源: 题型:

 小华从家里到学校的路是一段平路和一段下坡路,假设他始终保持平路每分钟走60
小华从家里到学校的路是一段平路和一段下坡路,假设他始终保持平路每分钟走60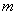 ,下坡路每分钟走80
,下坡路每分钟走80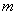 ,上坡路每分钟走40
,上坡路每分钟走40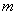 ,则他从家里到学校需10
,则他从家里到学校需10 ,从学校到家里需15
,从学校到家里需15 .问:从小华家到学校的平路和下坡路各有多远?
.问:从小华家到学校的平路和下坡路各有多远?

查看答案和解析>>
科目:初中数学 来源: 题型:
已知反比例函数y=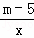 (m为常数,且m≠5).
(m为常数,且m≠5).
(1)若在其图象的每个分支上,y随x的增大而增大,求m的取值范围;
(2)若其图象与一次函数y=﹣x+1图象的一个交点的纵坐标是3,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
现有甲、乙两个合唱队队员的平均身高为170cm,方程分别是S甲2、S乙2,且S甲2>S乙2,则两个队的队员的身高较整齐的是( )
|
| A. | 甲队 | B. | 乙队 | C. | 两队一样整齐 | D. | 不能确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:
已知实数a,b在数轴上的位置如图所示,下列结论错误的是( )

|
| A. | |a|<1<|b| | B. | 1<﹣a<b | C. | 1<|a|<b | D. | ﹣b<a<﹣1 |

查看答案和解析>>
科目:初中数学 来源: 题型:
为弘扬“东亚文化”,某单位开展了“东亚文化之都”演讲比赛,在安排1位女选手和3位男选手的出场顺序时,采用随机抽签方式.
(1)请直接写出第一位出场是女选手的概率;
(2)请你用画树状图或列表的方法表示第一、二位出场选手的所有等可能结果,并求出他们都是男选手的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com