
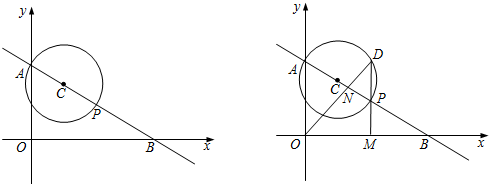
分析 (1)根据一次函数的解析式和坐标轴上点的坐标特征求出点A、B的坐标,根据余弦的定义计算即可;
(2)分⊙C过原点O和⊙C与OB相切两种情况,根据题意和切线的性质定理以及相似三角形的性质计算即可;
(3)连接AD,根据圆周角定理得到∠ADP=90°,证明∠ABO=∠AOD,根据正切的定义求出DA的长,在Rt△ADO中,根据余弦的定义求出AP,得到a的值.
解答 解:(1)∵直线y=-$\frac{5}{12}$x+5与x轴、y轴分别交于点A、B,
∴A (0,5),B (12,0),
∴AO=5,BO=12.
∵AO⊥BO,
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=13,
∴$cos∠ABO=\frac{BO}{AB}=\frac{12}{13}$;
(2)⊙C与坐标轴恰有3个公共点时,⊙C过原点O或⊙C与OB相切,
①⊙C过原点O,
∴a=AB=13;
②如图1,⊙C与OB相切,设切点为H,连接CH,则CH⊥OB,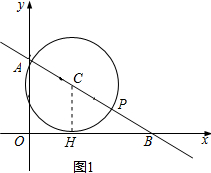
∵AO⊥OB,
∴△BCH∽△BAO,
∴$\frac{BC}{BA}=\frac{CH}{AO}$,
∴$\frac{{13-\frac{1}{2}a}}{13}=\frac{{\frac{1}{2}a}}{5}$,
∴$a=\frac{65}{9}$.
综上所述:a=13或$a=\frac{65}{9}$;
(3)如图2,连接AD,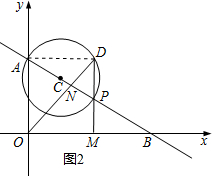
∵AP是直径,
∴∠ADP=90°,
∵PM⊥x轴,
∴∠DMB=90°.
∵∠ABO=∠ODM,∠NPD=∠BPM,
∴∠DNP=∠BMP=90°,
∴∠ABO=90°-∠DOM=∠AOD,
∴tan∠AOD=$tan∠ABO=\frac{AO}{BO}=\frac{5}{12}$,
PM⊥x轴,AO⊥x轴,∠ADP=90°,
∴∠OAD=90°,
在Rt△ADO中,tan∠AOD=$\frac{AD}{AO}$=$\frac{5}{12}$,
∴AD=$\frac{5}{12}$×5=$\frac{25}{12}$,
又∵∠DAP=∠ABO,
在Rt△ADO中,cos∠DAP=$\frac{AD}{AP}$,
∴AP=$\frac{AD}{cos∠DAP}=\frac{AD}{cos∠ABO}$=$\frac{25}{12}$×$\frac{13}{12}$=$\frac{325}{144}$,
∴$a=AP=\frac{325}{144}$.
点评 本题考查的是直线与圆的位置关系、锐角三角函数的定义,正确作出辅助线、掌握切线的性质定理和锐角三角函数的定义是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | $\frac{x^6}{x^2}={x^3}$ | B. | $\frac{x+m}{x+n}=\frac{m}{n}$ | C. | $\frac{-a+b}{c}=-\frac{a+b}{c}$ | D. | $\frac{1}{a}+\frac{1}{b}=\frac{a+b}{ab}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
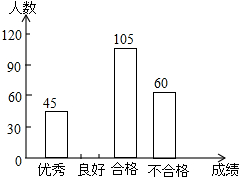 为了解今年初二学生的数学学习情况,某校在第一轮模拟测试后,对初二全体同学的数学成绩作了统计分析,绘制如图表:
为了解今年初二学生的数学学习情况,某校在第一轮模拟测试后,对初二全体同学的数学成绩作了统计分析,绘制如图表:| 成绩 | 频数 | 频率 |
| 优秀 | 45 | b |
| 良好 | a | 0.3 |
| 合格 | 105 | 0.35 |
| 不合格 | 60 | c |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 10° | B. | 15° | C. | 20° | D. | 25° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 程大位所著《算法统宗》是一部中国传统数学重要的著作.在《算法统宗》中记载:“平地秋千未起,踏板离地一尺.送行二步与人齐,五尺人高曾记.仕女佳人争蹴,终朝笑语欢嬉.良工高士素好奇,算出索长有几?”【注释】1步=5尺.
程大位所著《算法统宗》是一部中国传统数学重要的著作.在《算法统宗》中记载:“平地秋千未起,踏板离地一尺.送行二步与人齐,五尺人高曾记.仕女佳人争蹴,终朝笑语欢嬉.良工高士素好奇,算出索长有几?”【注释】1步=5尺.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
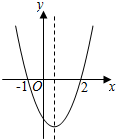 二次函数y=ax2+bx+c(a≠0)的大致图象如图所示,关于该二次函数,下列说法不正确的是( )
二次函数y=ax2+bx+c(a≠0)的大致图象如图所示,关于该二次函数,下列说法不正确的是( )| A. | 该函数有最小值 | B. | y随x的增大而减少 | ||
| C. | 对称轴是直线$x=\frac{1}{2}$ | D. | 当-1<x<2时,y《<0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com