
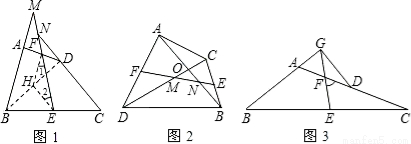
如图1,在四边形ABCD中,AB=CD,E、F分别是BC、AD的中点,连接EF并延长,分别与BA、CD的延长线交于点M、N,则∠BME=∠CNE(不需证明).
(温馨提示:在图1中,连接BD,取BD的中点H,连接HE、HF,根据三角形中位线定理,证明HE=HF,从而∠1=∠2,再利用平行线性质,可证得∠BME=∠CNE.)
问题一:如图2,在四边形ADBC中,AB与CD相交于点O,AB=CD,E、F分别是BC、AD的中点,连接EF,分别交DC、AB于点M、N,判断△OMN的形状,并说明理由;
问题二:如图3,在△ABC中,AC>AB,D点在AC上,AB=CD,E、F分别是BC、AD的中点,连接EF并延长,与BA的延长线交于点G,若∠EFC=60°,连接GD,判断△AGD的形状并并说明理由.
(1) △OMN为等腰三角形,理由见解析;(2)△AGD是直角三角形,理由见解析.
【解析】
试题分析:(1)作出两条中位线,根据中位线定理,找到相等的同位角和线段,进而判断出三角形的形状.
(2)利用平行线和中位线定理,可以证得三角形△FAG是等边三角形,再进一步确定∠FGD=∠FDG=30°,进而求出∠AGD=90°,故△AGD的形状可证.
试题解析::(1)取AC中点P,连接PF,PE,
可知PE=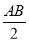 ,
,
PE∥AB,
∴∠PEF=∠ANF,
同理PF=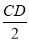 ,
,
PF∥CD,
∴∠PFE=∠CME,
又PE=PF,
∴∠PFE=∠PEF,
∴∠OMN=∠ONM,
∴△OMN为等腰三角形.
(2)判断出△AGD是直角三角形.
证明:如图连接BD,取BD的中点H,连接HF、HE,

∵F是AD的中点,
∴HF∥AB,HF=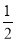 AB,
AB,
同理,HE∥CD,HE=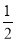 CD,
CD,
∵AB=CD
∴HF=HE,
∵∠EFC=60°,
∴∠HEF=60°,
∴∠HEF=∠HFE=60°,
∴△EHF是等边三角形,
∴∠3=∠EFC=∠AFG=60°,
∴△AGF是等边三角形.
∵AF=FD,
∴GF=FD,
∴∠FGD=∠FDG=30°
∴∠AGD=90°
即△AGD是直角三角形.
考点:1.三角形中位线定理;2.角平分线的性质;3.等腰三角形的判定;4.勾股定理的逆定理.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源:2015届江西省九年级上学期入学考试数学试卷(解析版) 题型:解答题
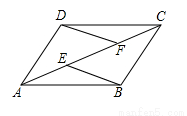
已知:如图,E、F是平行四边形ABCD的对角线AC上的两点,添加一个条件:____________,
可以得到DF=BE,DF∥BE.证明你的判断.
查看答案和解析>>
科目:初中数学 来源:2015届江西省八年级下学期第一次月考数学试卷(解析版) 题型:选择题
若一等腰三角形的腰长为4cm,腰上的高为2cm,则等腰三角形的顶角为( )
A.30° B.150° C.30°或150° D.以上都不对
查看答案和解析>>
科目:初中数学 来源:2015届江西省吉安市六校八年级下学期联考数学试卷(解析版) 题型:选择题
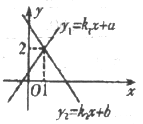
如图所示,直线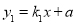 与
与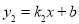 的交点坐标为(1,2)则使
的交点坐标为(1,2)则使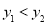 成立的x的取值范围为( )
成立的x的取值范围为( )
A.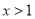 B.
B.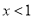 C.
C.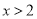 D.
D.
查看答案和解析>>
科目:初中数学 来源:2015届江苏省苏州市相城区八年级下学期期末考试数学试卷(解析版) 题型:解答题
为了构建城市立体道路网络,决定修建一条轻轨铁路,为了使工程提前6个月完成,需将原定的工作效率提高25%.原计划完成这项工程需要多少个月?
查看答案和解析>>
科目:初中数学 来源:2015届江苏省盐城市东台市八年级下学期第一次月考数学试卷(解析版) 题型:选择题
如图,下面不能判断是平行四边形的是( )
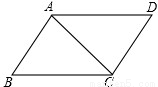
A.∠B=∠D,∠A=∠C
B.AB∥CD,AD∥BC
C.∠B+∠DAB=180°,∠B+∠BCD=180°
D.AB∥CD,AB=CD
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com