
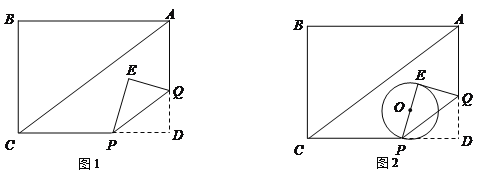
【题目】如图1,在矩形ABCD中,AD=3,DC=4,动点P在线段DC上以每秒1个单位的速度从点D向点C运动,过点P作PQ∥AC交AD于Q,将△PDQ沿PQ翻折得到△PQE. 设点P的运动时间为t(s).
(1)当点E落在边AB上时,t的值为 ;
(2)设△PQE与△ADC重叠部分的面积为s,求s与t的函数关系式;
(3)如图2,以PE为直径作⊙O.当⊙O与AC边相切时,求CP的长.
【答案】(1)![]() (2)s=
(2)s=![]() (当0<t≤2),s=
(当0<t≤2),s=![]() (2<t≤4)(3)
(2<t≤4)(3)![]()
【解析】分析:(1)过P作PF⊥BA于F,由∠QPD=∠ACD,得到∠QPD和∠ACD的三角函数相等,得到QD=![]() ,PQ=
,PQ=![]() ,EQ=QD=
,EQ=QD=![]() ,AQ=
,AQ=![]() .在△EFP中,由勾股定理得到EF=
.在△EFP中,由勾股定理得到EF=![]() ,由同角的余角相等,得到∠FEP=∠EQA,得到cos∠FEP=cos∠EQA,即
,由同角的余角相等,得到∠FEP=∠EQA,得到cos∠FEP=cos∠EQA,即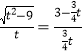 ,解方程即可得到结论;
,解方程即可得到结论;
(2)当E刚好在CA上时,如图3,由平行线的性质和折叠的性质得到∠1=∠4=∠2=∠3,得到PC=PE=PD=t,即2t=4,解方程即可.然后分两种情况讨论:
①当![]() 时, S=S△EPQ=S△PDQ即可得到结论;
时, S=S△EPQ=S△PDQ即可得到结论;
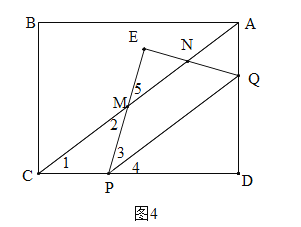
②当![]() 时,如图4,由(2)可知,PM=PC=4-t,得到EM=t-(4-t)=2t-4,由相似三角形的性质得到
时,如图4,由(2)可知,PM=PC=4-t,得到EM=t-(4-t)=2t-4,由相似三角形的性质得到![]() ,由 S=
,由 S=![]() 即可得到结论.
即可得到结论.
(3)如图,设切点为H,作PG⊥AC于G,连接HO并延长交PQ于F.设CP=5x,则PG=3x,PD=PE=4-5x,由OF= ![]() OP, 得到HF=OH+OF=
OP, 得到HF=OH+OF=![]() ( 4-5x ) ,从而得到
( 4-5x ) ,从而得到![]() ( 4-5x )=3x,求出x的值 ,由CP=5x即可得到结论.
( 4-5x )=3x,求出x的值 ,由CP=5x即可得到结论.
详解:(1)过P作PF⊥BA于F.在△ADC中,sin∠ACD=![]() ,cos∠ACD=
,cos∠ACD=![]() .∵PQ∥CA,∴∠QPD=∠ACD,tan∠ACD=
.∵PQ∥CA,∴∠QPD=∠ACD,tan∠ACD=![]() .∵PD=PE=t,∴QD=
.∵PD=PE=t,∴QD=![]() ,PQ=
,PQ=![]() ,∴EQ=QD=
,∴EQ=QD=![]() ,AQ=
,AQ=![]() .在△EFP中,∵PF=3,PE=t,∴EF=
.在△EFP中,∵PF=3,PE=t,∴EF=![]() .∵∠PEQ=90°,∴∠FEP+∠EPF=90°,∠AEQ+∠EQA=90°,∴∠FEP=∠EQA,∴cos∠FEP=cos∠EQA,∴
.∵∠PEQ=90°,∴∠FEP+∠EPF=90°,∠AEQ+∠EQA=90°,∴∠FEP=∠EQA,∴cos∠FEP=cos∠EQA,∴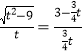 ,解得:t=
,解得:t=![]() ;
;

(2)当E刚好在CA上时,如图3.∵PQ∥CA,∴∠1=∠4,∠2=∠3.∵∠3=∠4,∴∠1=∠2,∴PC=PE.∵PE=PD=t,∴PC=PD=t,∴2t=4,解得:t=2.

①当![]() 时,如图1,S=S△EPQ=S△PDQ=
时,如图1,S=S△EPQ=S△PDQ=![]() PDQD=
PDQD=![]() =
=![]() ;
;

②当![]() 时,如图4,由(2)可知,PM=PC=4-t,∴EM=t-(4-t)=2t-4.∵AC∥PQ,∴△EMN∽△EPQ,∴
时,如图4,由(2)可知,PM=PC=4-t,∴EM=t-(4-t)=2t-4.∵AC∥PQ,∴△EMN∽△EPQ,∴![]() .∵S△EPQ=S△PDQ=
.∵S△EPQ=S△PDQ=![]() PDQD=
PDQD=![]() =
=![]() ,∴
,∴![]() ,∴S=
,∴S=![]() =
=![]() -
-![]() =
=![]() .
.
综上所述:S=
(3)如图,设切点为H,作PG⊥AC于G,连接HO并延长交PQ于F.
设CP=5x,则PG=3x,PD=PE=4-5x,
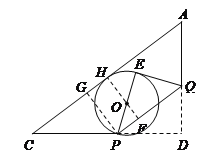
∵OF= ![]() OP, ∴HF=OH+OF=OP+OF=
OP, ∴HF=OH+OF=OP+OF=![]() OP=
OP=![]() PD=
PD=![]() ( 4-5x )
( 4-5x )
∴![]() ( 4-5x )=3x,解得:x=
( 4-5x )=3x,解得:x=![]() ,∴CP=5x=
,∴CP=5x=![]() .
.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】将连续的奇数1、3、5、7、9,……排成如下的数表:
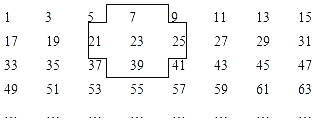
(1)十字框中的5个数的和与中间的数23有什么关系?若将十字框上下左右平移,可框住另外5个数,这5个数还有这种规律吗?
(2)设十字框中中间的数为a,用含a的式子表示十字框中的其他四个数;
(3)十字框中的5个数的和能等于2018吗?若能,请写出这5个数;若不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是张亮、李娜两位同学零花钱全学期各项支出的统计图.根据统计图,下列对两位同学购买书籍支出占全学期总支出的百分比作出的判断中,正确的是( )


A. 张亮的百分比比李娜的百分比大 B. 张娜的百分比比张亮的百分比大
C. 张亮的百分比与李娜的百分比一样大 D. 无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表是某校七年级小朋友小敏这学期第一周和第二周做家务事的时间统计表,已知小敏每次在做家务事中洗碗的时间相同,扫地的时间也相同.
每周做家务总时间(分) | 洗碗次数 | 扫地的次数 | |
第一周 | 44 | 2 | 3 |
第二周 | 42 | 1 | 4 |
(1)求小敏每次洗碗的时间和扫地的时间各是多少?
(2)为鼓励小敏做家务,小敏的家长准备洗碗一次付12元,扫地一次付8元,总费用不超过100元。请问小敏如何安排洗碗与扫地的次数,既能够让花费的总时间最少,又能够全部拿到100元?
查看答案和解析>>
科目:初中数学 来源: 题型:
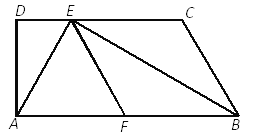
【题目】如图,已知梯形ABCD中,AB∥CD,∠D=90°,BE平分∠ABC,交CD于点E,F是AB的中点,联结AE、EF,且AE⊥BE.
求证:(1)四边形BCEF是菱形;
(2)![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC为直角三角形,∠C=90°,BC=2cm,∠A=30°,四边形DEFG为矩形,DE=2![]() cm,EF=6cm,且点C、B、E、F在同一条直线上,点B与点E重合.Rt△ABC以每秒1cm的速度沿矩形DEFG的边EF向右平移,当点C与点F重合时停止.设Rt△ABC与矩形DEFG的重叠部分的面积为ycm2,运动时间xs.能反映ycm2与xs之间函数关系的大致图象是( )
cm,EF=6cm,且点C、B、E、F在同一条直线上,点B与点E重合.Rt△ABC以每秒1cm的速度沿矩形DEFG的边EF向右平移,当点C与点F重合时停止.设Rt△ABC与矩形DEFG的重叠部分的面积为ycm2,运动时间xs.能反映ycm2与xs之间函数关系的大致图象是( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车交易市场为了解二手轿车的交易情况,将本市场去年成交的二手轿车的全部数据,以二手轿车交易前的使用时间为标准分为A、B、C、D、E五类,并根据这些数据由甲,乙两人分别绘制了下面的两幅统计图(图都不完整).

请根据以上信息,解答下列问题:
(1)该汽车交易市场去年共交易二手轿车 辆.
(2)把这幅条形统计图补充完整.(画图后请标注相应的数据)
(3)在扇形统计图中,D类二手轿车交易辆数所对应扇形的圆心角为 度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点![]() 是反比例函数
是反比例函数![]()
![]() 的图象上一点过点
的图象上一点过点![]() 作
作![]() 轴于点
轴于点![]() ,连结
,连结![]() ,
,![]() 的面积为
的面积为![]() .
.
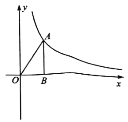
(1)求![]() 和
和![]() 的值.
的值.
(2)直线![]() 与
与![]() 的延长线交于点
的延长线交于点![]() ,与反比例函数图象交于点
,与反比例函数图象交于点![]() .
.
①若![]() ,求点
,求点![]() 坐标;②若点
坐标;②若点![]() 到直线
到直线![]() 的距离等于
的距离等于![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com