
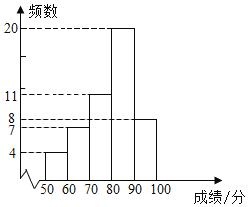
【题目】为了解某社区居民掌握民法知识的情况,对社区内的甲、乙两个小区各500名居民进行了测试,从中各随机抽取50名居民的成绩(百分制)进行整理、描述、分析,得到部分信息:
a.甲小区50名居民成绩的频数直方图如下(数据分成5组:50≤x<60,60≤x<70,70≤x<80,80≤x<90,90≤x≤100);
b.图中,70≤x<80组的前5名的成绩是:79 79 79 78 77
c.图中,80≤x<90组的成绩如下:
82 | 83 | 84 | 85 | 85 | 86 | 86 | 86 | 86 | 86 |
86 | 86 | 86 | 87 | 87 | 87 | 88 | 88 | 89 | 89 |
d.两组样本数据的平均数、中位数、众数、优秀率(85分及以上)、满分人数如下表所示:
小区 | 平均数 | 中位数 | 众数 | 优秀率 | 满分人数 |
甲 | 78.58 | 84.5 | a | b | 1 |
乙 | 76.92 | 79.5 | 90 | 40% | 4 |
根据以上信息,回答下列问题:
(1)求表中a,b的值;
(2)请估计甲小区500名居民成绩能超过平均数的人数;
(3)请尽量从多个角度,分析甲、乙两个小区参加测试的居民掌握民法知识的情况.
【答案】(1)86;50% (2)310人 (3)见解析
【解析】
(1)由众数的定义和优秀率的计算公式可求解;
(2)A小区500名居民成绩能超过平均数的人数:500×![]() =310(人);
=310(人);
(3)根据统计量:平均数、中位数、众数、优秀率,即可分析甲、乙两小区参加测试的居民掌握民法知识的情况.
解:(1)∵86出现的次数最多,
∴众数a=86,
优秀率b=![]() ×100%=50%;
×100%=50%;
(2)500×![]() =310(人),
=310(人),
答:甲小区500名居民成绩能超过平均数的人数为310人;
(3)从平均数看,甲小区居民掌握民法知识平均分比乙小区居民掌握民法知识的平均分高;
从中位数看,甲小区居民掌握民法知识的情况比乙小区居民掌握民法知识的情况好;
从众数看,乙小区居民掌握民法知识的情况比甲小区居民掌握民法知识的情况好;
从优秀率看,甲小区居民掌握民法知识的成绩优秀率比乙小区居民掌握民法知识的成绩优秀率高.


科目:初中数学 来源: 题型:
【题目】已知二次函数图象过点A(-2,0),B(4,0),C(0,4)
(1)求二次函数的解析式;
(2)如图,当点P为AC的中点时,在线段PB上是否存在点M,使得∠BMC=90°?若存在,求出点M的坐标,若不存在,请说明理由.
(3)点K在抛物线上,点D为AB的中点,直线KD与直线BC的夹角为锐角![]() ,且tan
,且tan![]() =
=![]() ,求点K的坐标.
,求点K的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年植树节期间,某景观园林公司购进一批成捆的![]() ,
,![]() 两种树苗,每捆
两种树苗,每捆![]() 种树苗比每捆
种树苗比每捆![]() 种树苗多10棵,每捆
种树苗多10棵,每捆![]() 种树苗和每捆
种树苗和每捆![]() 种树苗的价格分别是630元和600元,而每棵
种树苗的价格分别是630元和600元,而每棵![]() 种树苗和每棵
种树苗和每棵![]() 种树苗的价格分别是这一批树苗平均每棵价格的0.9倍和1.2倍.
种树苗的价格分别是这一批树苗平均每棵价格的0.9倍和1.2倍.
(1)求这一批树苗平均每棵的价格是多少元?
(2)如果购进的这批树苗共5500棵,![]() 种树苗至多购进3500棵,为了使购进的这批树苗的费用最低,应购进
种树苗至多购进3500棵,为了使购进的这批树苗的费用最低,应购进![]() 种树苗和
种树苗和![]() 种树苗各多少棵?并求出最低费用.
种树苗各多少棵?并求出最低费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
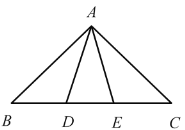
【题目】古希腊数学家欧多克索斯在深入研究比例理论时,提出了分线段的“中末比”问题:点G将一线段![]() 分为两线段
分为两线段![]() ,
,![]() ,使得其中较长的一段
,使得其中较长的一段![]() 是全长
是全长![]() 与较短的段
与较短的段![]() 的比例中项,即满足
的比例中项,即满足![]() ,后人把
,后人把![]() 这个数称为“黄金分割”数,把点G称为线段
这个数称为“黄金分割”数,把点G称为线段![]() 的“黄金分割”点.如图,在
的“黄金分割”点.如图,在![]() 中,已知
中,已知![]() ,
,![]() ,若D,E是边
,若D,E是边![]() 的两个“黄金分割”点,则
的两个“黄金分割”点,则![]() 的面积为( )
的面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 经过
经过![]() ,
,![]() ,
,![]() 三点.
三点.
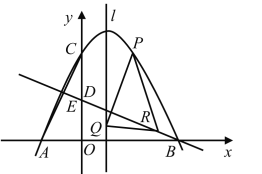
(1)求该抛物线的解析式;
(2)经过点B的直线交y轴于点D,交线段![]() 于点E,若
于点E,若![]() .
.
①求直线![]() 的解析式;
的解析式;
②已知点Q在该抛物线的对称轴l上,且纵坐标为1,点P是该抛物线上位于第一象限的动点,且在l右侧.点R是直线![]() 上的动点,若
上的动点,若![]() 是以点Q为直角顶点的等腰直角三角形,求点P的坐标.
是以点Q为直角顶点的等腰直角三角形,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠C=90°,AC=BC,点P在线段BA的延长线上,作PD⊥AC,交AC的延长线于点D,点D关于直线AB的对称点为E,连接PE并延长PE到点F,使EF=AC,连接CF.
(1)依题意补全图1;
(2)求证:AD=CF;
(3)若AC=2,点Q在直线AB上,写出一个AQ的值,使得对于任意的点P总有QD=QF,并证明.
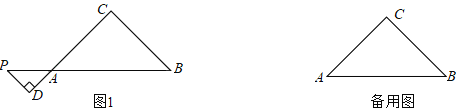
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小丽为更好的掌握一元二次方程根的判断情况,两人玩一个游戏:
在一个不透明口袋中装有分别标有 -1,0,1,2的四个小球,除了数字不同之外,这些小球完全一样.
(1)从中任取1球,此小球是非负数的概率是__________.
(2)小明从四球中任取两球,数字和记为m,若一元二次方程![]() 有实根,小明赢,无实根小丽赢.这个游戏公平吗?请你用树状图或列举法分别求出小明、小丽赢的概率,并说明理由.
有实根,小明赢,无实根小丽赢.这个游戏公平吗?请你用树状图或列举法分别求出小明、小丽赢的概率,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近几年,国内快递业务快速发展,由于其便捷、高效,人们越来越多地通过快递公司代办点来代寄包裹.某快递公司某地区一代办点对60天中每天代寄的包裹数与天数的数据(每天代寄包裹数、天数均为整数)统计如下:
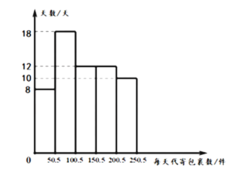
(1)求该数据中每天代寄包裹数在![]() 范围内的天数;
范围内的天数;
(2)若该代办点对顾客代寄包裹的收费标准为:重量小于或等于1千克的包裹收费8元;重量超1千克的包裹,在收费8元的基础上,每超过1千克(不足1千克的按1千克计算)需再收取2元.
①某顾客到该代办点寄重量为1.6千克的包裹,求该顾客应付多少元费用?
②这60天中,该代办点为顾客代寄的包表中有一部分重量超过2千克,且不超过5千克.现从中随机抽取40件包裹的重量数据作为样本,统计如下:
重量G(单位:千克) |
|
|
|
件数(单位:件) | 15 | 10 | 15 |
求这40件包裹收取费用的平均数.
查看答案和解析>>
科目:初中数学 来源: 题型:
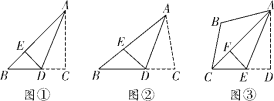
【题目】(1)操作发现
如图①,在![]() 中,
中,![]() ,点D是
,点D是![]() 上一点,沿
上一点,沿![]() 折叠
折叠![]() ,使得点C恰好落在
,使得点C恰好落在![]() 上的点E处.则
上的点E处.则![]() 的数量关系为______;
的数量关系为______;![]() ________;
________;
(2)问题解决
如图②,若(1)中![]() ,其他条件不变,请猜想
,其他条件不变,请猜想![]() 之间的关系,并证明你的结论;
之间的关系,并证明你的结论;
(3)类比探究
如图③,在四边形![]() 中,
中,![]() ,连接
,连接![]() ,点E是
,点E是![]() 上一点,沿
上一点,沿![]() 折叠
折叠![]() 使得点D正好落在
使得点D正好落在![]() 上的点F处,若
上的点F处,若![]() ,直接写出
,直接写出![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com