
【题目】古希腊数学家欧多克索斯在深入研究比例理论时,提出了分线段的“中末比”问题:点G将一线段![]() 分为两线段
分为两线段![]() ,
,![]() ,使得其中较长的一段
,使得其中较长的一段![]() 是全长
是全长![]() 与较短的段
与较短的段![]() 的比例中项,即满足
的比例中项,即满足![]() ,后人把
,后人把![]() 这个数称为“黄金分割”数,把点G称为线段
这个数称为“黄金分割”数,把点G称为线段![]() 的“黄金分割”点.如图,在
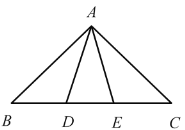
的“黄金分割”点.如图,在![]() 中,已知
中,已知![]() ,
,![]() ,若D,E是边
,若D,E是边![]() 的两个“黄金分割”点,则
的两个“黄金分割”点,则![]() 的面积为( )
的面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
科目:初中数学 来源: 题型:
【题目】(教材呈现)
下图是华师版九年级上册数学教材第79页的部分内容.
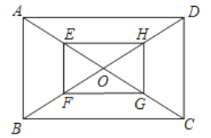
如图,矩形![]() 的对角线
的对角线![]() 、
、![]() 相交于点
相交于点![]() ,
,![]() 、
、![]() 、
、![]() 、
、![]() 分别为
分别为![]() 、
、![]() 、
、![]() 、
、![]() 的中点,求证:四边形
的中点,求证:四边形![]() 是矩形.
是矩形.
请根据教材内容,结合图①,写出完整的解题过程.
(结论应用)
(1)在图①中,若![]() ,
,![]() ,则四边形
,则四边形![]() 的面积为__________;
的面积为__________;
(2)如图②,在菱形![]() 中,
中,![]() ,
,![]() 是其内任意一点,连接
是其内任意一点,连接![]() 与菱形
与菱形![]() 各顶点,四边形
各顶点,四边形![]() 的顶点
的顶点![]() 、
、![]() 、
、![]() 、
、![]() 分别在
分别在![]() 、
、![]() 、
、![]() 、
、![]() 上,
上,![]() ,
,![]() ,且
,且![]() ,若
,若![]() 与
与![]() 的面积和为
的面积和为![]() ,则菱形
,则菱形![]() 的周长为___________.
的周长为___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A(﹣6,0),点B(0,8),点C在线段AB上,点D在y轴上,将∠ABO沿直线CD翻折,使点B与点A重合.若点E在线段CD延长线上,且CE=5,点M在y轴上,点N在坐标平面内,如果以点C、E、M、N为顶点的四边形是菱形,那么点N有( )
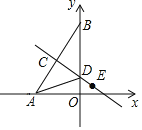
A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了丰富同学们的课余生活,冬威中学开展以“我最喜欢的课外活动小组”为主题的调查活动,围绕在绘画、剪纸、舞蹈、书法四类活动小组中,你最喜欢的哪一类?的问题,在全校范围内随机抽取部分学生进行问卷调查,将调查结果整理后绘制成如图所示的不完整的条形统计图,其中最喜欢绘画小组的学生人数占所调查人数的![]() ,请你根据图中提供的信息回答下列问题:
,请你根据图中提供的信息回答下列问题:

(1)在这次调查中,一共抽取了多少名学生;
(2)请通过计算补全条形统计图;
(3)若冬威中学共有800名学生,请你估计该中学最喜欢剪纸小组的学生有多少名.
查看答案和解析>>
科目:初中数学 来源: 题型:
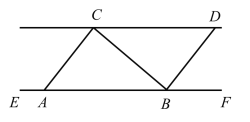
【题目】如图,为了测量某条河的对岸边C,D两点间的距离,在河的岸边与![]() 平行的直线
平行的直线![]() 上取两点A,B,测得
上取两点A,B,测得![]() ,
,![]()
![]() ,量得
,量得![]() 长为70米.求C,D两点间的距离(参考数据:
长为70米.求C,D两点间的距离(参考数据:![]() ,
,![]() ,
,![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
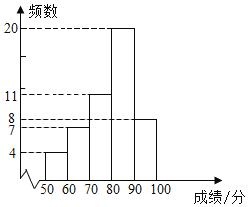
【题目】为了解某社区居民掌握民法知识的情况,对社区内的甲、乙两个小区各500名居民进行了测试,从中各随机抽取50名居民的成绩(百分制)进行整理、描述、分析,得到部分信息:
a.甲小区50名居民成绩的频数直方图如下(数据分成5组:50≤x<60,60≤x<70,70≤x<80,80≤x<90,90≤x≤100);
b.图中,70≤x<80组的前5名的成绩是:79 79 79 78 77
c.图中,80≤x<90组的成绩如下:
82 | 83 | 84 | 85 | 85 | 86 | 86 | 86 | 86 | 86 |
86 | 86 | 86 | 87 | 87 | 87 | 88 | 88 | 89 | 89 |
d.两组样本数据的平均数、中位数、众数、优秀率(85分及以上)、满分人数如下表所示:
小区 | 平均数 | 中位数 | 众数 | 优秀率 | 满分人数 |
甲 | 78.58 | 84.5 | a | b | 1 |
乙 | 76.92 | 79.5 | 90 | 40% | 4 |
根据以上信息,回答下列问题:
(1)求表中a,b的值;
(2)请估计甲小区500名居民成绩能超过平均数的人数;
(3)请尽量从多个角度,分析甲、乙两个小区参加测试的居民掌握民法知识的情况.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与x轴交于A,与y轴交于B,抛物线
与x轴交于A,与y轴交于B,抛物线![]() 经过点A,且与y轴交于点C(0,4),P为x轴上一动点,按逆时针方向作CPE,使CPE∽AOB.
经过点A,且与y轴交于点C(0,4),P为x轴上一动点,按逆时针方向作CPE,使CPE∽AOB.
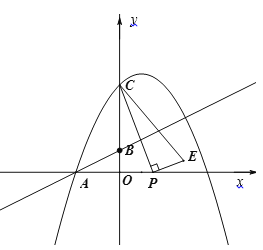
(1)求抛物线解析式.
(2)若点E落在抛物线上,求出点P的坐标.
(3)若ABE是直角三角形,直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春节期间,某商场计划购进甲、乙两种商品,已知购进甲商品2件和乙商品3件共需270元;购进甲商品3件和乙商品2件共需230元.
(1)求甲、乙两种商品每件的进价分别是多少元?
(2)商场决定甲商品以每件40元出售,乙商品以每件90元出售,为满足市场需求,需购进甲、乙两种商品共100件,且甲种商品的数量不少于乙种商品数量的4倍,请你求出获利最大的进货方案,并确定最大利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com