
【题目】今年植树节期间,某景观园林公司购进一批成捆的![]() ,
,![]() 两种树苗,每捆
两种树苗,每捆![]() 种树苗比每捆
种树苗比每捆![]() 种树苗多10棵,每捆
种树苗多10棵,每捆![]() 种树苗和每捆
种树苗和每捆![]() 种树苗的价格分别是630元和600元,而每棵
种树苗的价格分别是630元和600元,而每棵![]() 种树苗和每棵
种树苗和每棵![]() 种树苗的价格分别是这一批树苗平均每棵价格的0.9倍和1.2倍.
种树苗的价格分别是这一批树苗平均每棵价格的0.9倍和1.2倍.
(1)求这一批树苗平均每棵的价格是多少元?
(2)如果购进的这批树苗共5500棵,![]() 种树苗至多购进3500棵,为了使购进的这批树苗的费用最低,应购进
种树苗至多购进3500棵,为了使购进的这批树苗的费用最低,应购进![]() 种树苗和
种树苗和![]() 种树苗各多少棵?并求出最低费用.
种树苗各多少棵?并求出最低费用.
【答案】(1)这一批树苗平均每棵的价格是20元;(2)购进![]() 种树苗3500棵,
种树苗3500棵,![]() 种树苗2000棵,能使得购进这批树苗的费用最低为111000元.
种树苗2000棵,能使得购进这批树苗的费用最低为111000元.
【解析】
(1)设这一批树苗平均每棵的价格是![]() 元,分别表示出两种树苗的数量,根据“每捆
元,分别表示出两种树苗的数量,根据“每捆![]() 种树苗比每捆
种树苗比每捆![]() 种树苗多10棵”列方程即可求解;
种树苗多10棵”列方程即可求解;
(2)设购进![]() 种树苗
种树苗![]() 棵,这批树苗的费用为
棵,这批树苗的费用为![]() ,得到w与t的关系式,根据题意得到t的取值范围,根据函数增减性即可求解.
,得到w与t的关系式,根据题意得到t的取值范围,根据函数增减性即可求解.
解:(1)设这一批树苗平均每棵的价格是![]() 元,
元,
根据题意,得![]() ,
,
解之,得![]() .
.
经检验知,![]() 是原分式方程的根,并符合题意.
是原分式方程的根,并符合题意.
答:这一批树苗平均每棵的价格是20元.
(2)由(1)可知![]() 种树苗每棵价格为
种树苗每棵价格为![]() 元,种树苗每棵价格为
元,种树苗每棵价格为![]() 元,
元,
设购进![]() 种树苗
种树苗![]() 棵,这批树苗的费用为
棵,这批树苗的费用为![]() ,则
,则
![]() .
.
∵![]() 是
是![]() 的一次函数,
的一次函数,![]() ,
,![]() 随着
随着![]() 的增大而减小,
的增大而减小,![]() ,
,
∴当![]() 棵时,
棵时,![]() 最小.此时,
最小.此时,![]() 种树苗有
种树苗有![]() 棵,
棵,![]() .
.
答:购进![]() 种树苗3500棵,
种树苗3500棵,![]() 种树苗2000棵,能使得购进这批树苗的费用最低为111000元.
种树苗2000棵,能使得购进这批树苗的费用最低为111000元.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】“保护生态环境,建设绿色社会”已经从理念变为人们的行动,某化工厂2018年1月的利润为200万元.设2018年1月为第1个月,第x个月的利润为y万元.由于排污超标,该厂决定从2018年1月底起适当限产,并投入资金进行治污改造,导致月利润明显下降,从1月到5月,y与x成反比例.到5月底,治污改造工程顺利完工,从这时起,该厂每月的利润比前一个月增加20万元(如图).
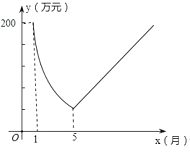
(1)分别求该化工厂治污期间及治污改造工程完工后,y与x之间对应的函数关系式.
(2)治污改造工程完工后经过几个月,该厂月利润才能达到2018年1月的水平?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了科学普及新型冠状病毒肺炎防护知识,提升学生的自我防护意识和能力,某中学开展线上“战疫情复课复学”科普知识竞赛活动,竞赛试卷满分100分.活动结束后,从参赛的七年级学生中随机抽取了30名同学的成绩(单位:分),收集数据如下:
91,93,88,79,92,82,93,93,98,98,89,96,78,100,93,
98,95,93,96,88,99,98,75,80,86,92,90,88,96,93
并将数据整理后,绘制以下不完整的统计表(图1)、频数分布直方图(图2)和扇形统计图(图3).
请根据图表中的信息解答下列各题:
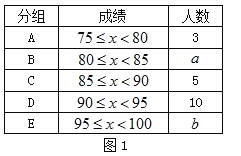
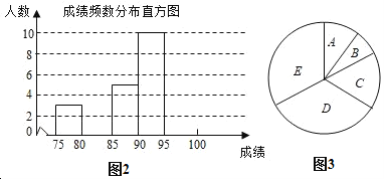
(1)填空:![]() ________,
________,![]() ________;
________;
(2)补全频数分布直方图.若成绩在“85分到90分以下”为“成绩良好”,请你求出扇形统计图中“成绩良好”部分的圆心角的度数;
(3)成绩达到“90分及以上”为“成绩优秀”.现需分别从![]() 组的甲、乙和
组的甲、乙和![]() 组的丙、丁四位同学中,随机选取两人参加全校决赛,请用画树状图或列表法求出选中的两人恰好是在同一个小组的概率.
组的丙、丁四位同学中,随机选取两人参加全校决赛,请用画树状图或列表法求出选中的两人恰好是在同一个小组的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
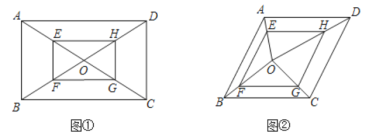
【题目】(教材呈现)
下图是华师版九年级上册数学教材第79页的部分内容.
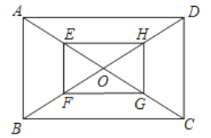
如图,矩形![]() 的对角线
的对角线![]() 、
、![]() 相交于点
相交于点![]() ,
,![]() 、
、![]() 、
、![]() 、
、![]() 分别为
分别为![]() 、
、![]() 、
、![]() 、
、![]() 的中点,求证:四边形
的中点,求证:四边形![]() 是矩形.
是矩形.
请根据教材内容,结合图①,写出完整的解题过程.
(结论应用)
(1)在图①中,若![]() ,
,![]() ,则四边形
,则四边形![]() 的面积为__________;
的面积为__________;
(2)如图②,在菱形![]() 中,
中,![]() ,
,![]() 是其内任意一点,连接
是其内任意一点,连接![]() 与菱形
与菱形![]() 各顶点,四边形
各顶点,四边形![]() 的顶点
的顶点![]() 、
、![]() 、
、![]() 、
、![]() 分别在
分别在![]() 、
、![]() 、
、![]() 、
、![]() 上,
上,![]() ,
,![]() ,且
,且![]() ,若
,若![]() 与
与![]() 的面积和为
的面积和为![]() ,则菱形
,则菱形![]() 的周长为___________.
的周长为___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平而直角坐标系中,已知点![]() ,直线
,直线![]() 经过点
经过点![]() .抛物线
.抛物线![]() 恰好经过
恰好经过![]() 三点中的两点.
三点中的两点.
![]() 判断点
判断点![]() 是否在直线
是否在直线![]() 上.并说明理由;
上.并说明理由;
![]() 求
求![]() 的值;
的值;
![]() 平移抛物线
平移抛物线![]() ,使其顶点仍在直线
,使其顶点仍在直线![]() 上,求平移后所得抛物线与
上,求平移后所得抛物线与![]() 轴交点纵坐标的最大值.
轴交点纵坐标的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A(﹣6,0),点B(0,8),点C在线段AB上,点D在y轴上,将∠ABO沿直线CD翻折,使点B与点A重合.若点E在线段CD延长线上,且CE=5,点M在y轴上,点N在坐标平面内,如果以点C、E、M、N为顶点的四边形是菱形,那么点N有( )
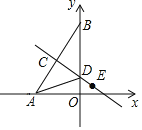
A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了丰富同学们的课余生活,冬威中学开展以“我最喜欢的课外活动小组”为主题的调查活动,围绕在绘画、剪纸、舞蹈、书法四类活动小组中,你最喜欢的哪一类?的问题,在全校范围内随机抽取部分学生进行问卷调查,将调查结果整理后绘制成如图所示的不完整的条形统计图,其中最喜欢绘画小组的学生人数占所调查人数的![]() ,请你根据图中提供的信息回答下列问题:
,请你根据图中提供的信息回答下列问题:

(1)在这次调查中,一共抽取了多少名学生;
(2)请通过计算补全条形统计图;
(3)若冬威中学共有800名学生,请你估计该中学最喜欢剪纸小组的学生有多少名.
查看答案和解析>>
科目:初中数学 来源: 题型:
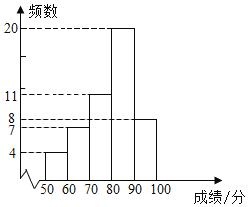
【题目】为了解某社区居民掌握民法知识的情况,对社区内的甲、乙两个小区各500名居民进行了测试,从中各随机抽取50名居民的成绩(百分制)进行整理、描述、分析,得到部分信息:
a.甲小区50名居民成绩的频数直方图如下(数据分成5组:50≤x<60,60≤x<70,70≤x<80,80≤x<90,90≤x≤100);
b.图中,70≤x<80组的前5名的成绩是:79 79 79 78 77
c.图中,80≤x<90组的成绩如下:
82 | 83 | 84 | 85 | 85 | 86 | 86 | 86 | 86 | 86 |
86 | 86 | 86 | 87 | 87 | 87 | 88 | 88 | 89 | 89 |
d.两组样本数据的平均数、中位数、众数、优秀率(85分及以上)、满分人数如下表所示:
小区 | 平均数 | 中位数 | 众数 | 优秀率 | 满分人数 |
甲 | 78.58 | 84.5 | a | b | 1 |
乙 | 76.92 | 79.5 | 90 | 40% | 4 |
根据以上信息,回答下列问题:
(1)求表中a,b的值;
(2)请估计甲小区500名居民成绩能超过平均数的人数;
(3)请尽量从多个角度,分析甲、乙两个小区参加测试的居民掌握民法知识的情况.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图直角坐标系中,以M(3,0)为圆心的⊙M交x轴负半轴于A,交x轴正半轴于B,交y轴于C、D.
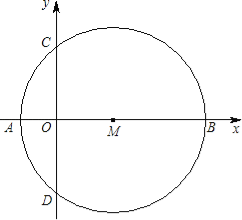
(1)若C点坐标为(0,4),求点A坐标.
(2)在(1)的条件下,在⊙M上,是否存在点P,使∠CPM=45°,若存在,求出满足条件的点P.
(3)过C作⊙M的切线CE,过A作AN⊥CE于F,交⊙M于N,当⊙M的半径大小发生变化时.AN的长度是否变化?若变化,求变化范围,若不变,证明并求值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com