
【题目】一位无线电爱好者把天线杆设在接收效果最佳的矩形屋顶之上.然后,他从杆顶到屋顶四角之间安装固定用的支撑线.有两根相对的支撑线分别长7米和4米,另一根长1米,则最后一根的长度应为( )
A. 8米 B. 9米 C. 10米 D. 12米
科目:初中数学 来源: 题型:
【题目】甲、乙两名射击运动员在某次训练中各射击10发子弹,成绩如表:
甲 | 8 | 9 | 7 | 9 | 8 | 6 | 7 | 8 | 10 | 8 |
乙 | 6 | 7 | 9 | 7 | 9 | 10 | 8 | 7 | 7 | 10 |
且![]() =8,S乙2=1.8,S甲2=1.2,根据上述信息完成下列问题:
=8,S乙2=1.8,S甲2=1.2,根据上述信息完成下列问题:
(1)乙运动员射击训练成绩的众数是 ,中位数是 .
(2)求甲运动员射击成绩的平均数,并判断甲、乙两人在本次射击成绩的稳定性.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用两种方法证明“直角三角形斜边上的中线等于斜边的一半”.
已知:如图1,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线.
求证:CD= ![]() AB.
AB.
证法1:如图2,在∠ACB的内部作∠BCE=∠B,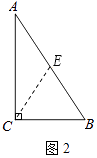
CE与AB相交于点E.
∵∠BCE=∠B,
∴ .
∵∠BCE+∠ACE=90°,
∴∠B+∠ACE=90°.
又∵ ,
∴∠ACE=∠A.
∴EA=EC.
∴EA=EB=EC,
即CE是斜边AB上的中线,且CE= ![]() AB.
AB.
又∵CD是斜边AB上的中线,即CD与CE重合,
∴CD= ![]() AB.
AB.
请把证法1补充完整,并用不同的方法完成证法2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“智慧南京、绿色出行”,骑共享单车出行已经成为一种时尚.记者随机调查了一些骑共享单车的秦淮区市民,并将他们对各种品牌单车的选择情况绘制成图①和图②的统计图(A:摩拜单车;B:ofo单车;C:HelloBike).请根据图中提供的信息,解答下列问题: 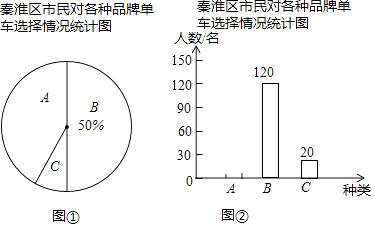
(1)在图①中,C部分所占扇形的圆心角度数为°;
(2)将图②补充完整;
(3)根据抽样调查结果,请你估计某天该区48万名骑共享单车的市民中有多少名选择摩拜单车?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一列快车和一列慢车同时从甲地出发,分别以速度v1、v2(单位:km/h,且v1>2v2)匀速驶向乙地.快车到达乙地后停留了2h,沿原路仍以速度v1匀速返回甲地.设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示从慢车出发至慢车到达乙地的过程中,y与x之间的函数关系.根据图象进行以下探究: 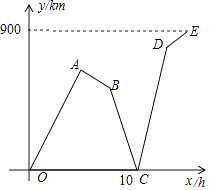
(1)甲、乙两地之间的距离为km;
(2)求线段AB、CD所表示的y与x之间的函数表达式;
(3)慢车出发多长时间后,两车相距480km?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、B、C分别是⊙O上的点,∠B=60°,AC=3,CD是⊙O的直径,P是CD延长线上的一点,且AP=AC. 
(1)求证:AP是⊙O的切线;
(2)求PD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,分别以点A和点B为圆心,以相同的长(大于 ![]() AB)为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交BC于点E.若AC=3,AB=5,则DE等于( )
AB)为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交BC于点E.若AC=3,AB=5,则DE等于( ) 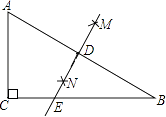
A.2
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八年级(1)班研究性学习小组为研究全校同学课外阅读情况,在全校随机邀请了部分同学参与问卷调查,统计同学们一个月阅读课外书的数量,并绘制了以下统计图.

请根据图中信息解决下列问题:
(1)共有多少名同学参与问卷调查;
(2)补全条形统计图和扇形统计图;
(3)全校共有学生1500人,请估计该校学生一个月阅读2本课外书的人数约为多少.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com