

 通城学典默写能手系列答案
通城学典默写能手系列答案科目:初中数学 来源: 题型:
| A、点A表示的数一定是整数 |
| B、点A表示的数一定是分数 |
| C、点A表示的数一定是有理数 |
| D、点A表示的数可能是无理数 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、0.8×107 |
| B、8×107 |
| C、8×106 |
| D、80×106 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
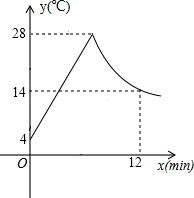 如图所示,制作某种食品的同时需将原材料加热,设该材料温度为y℃,从加热开始计算的时间为x分钟.据了解,该材料在加热过程中温度y与时间x成一次函数关系.已知该材料在加热前的温度为4℃,加热一段时间使材料温度达到28℃时停止加热,停止加热后,材料温度逐渐下降,这时温度y与时间x成反比例函数关系,已知当第12分钟时,材料温度是14℃.
如图所示,制作某种食品的同时需将原材料加热,设该材料温度为y℃,从加热开始计算的时间为x分钟.据了解,该材料在加热过程中温度y与时间x成一次函数关系.已知该材料在加热前的温度为4℃,加热一段时间使材料温度达到28℃时停止加热,停止加热后,材料温度逐渐下降,这时温度y与时间x成反比例函数关系,已知当第12分钟时,材料温度是14℃.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
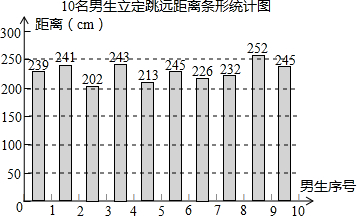
| 距离(cm) | 250 | 240 | 230 | 220 | 210 | 200 | … |
| 得分(分) | 15 | 14 | 13 | 12 | 11 | 10 | … |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com