
| BC |
| BP |
| BD |
| BC |
| BC |
| BP |
| BD |
| BC |


科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
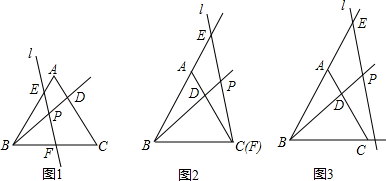
 如图,在△ABC中,AD平分∠BAC,P为线段AD上的一个动点,PE⊥AD交直线BC于点E.
如图,在△ABC中,AD平分∠BAC,P为线段AD上的一个动点,PE⊥AD交直线BC于点E.查看答案和解析>>
科目:初中数学 来源: 题型:
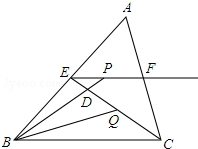 如图所示,在△ABC中,E、F分别是AB、AC的中点,BC=6,CE=5,动点P在射线EF上,BP交CE于D,∠CBP的平分线交CE于Q,当EP+BP=18时,则CQ的值为
如图所示,在△ABC中,E、F分别是AB、AC的中点,BC=6,CE=5,动点P在射线EF上,BP交CE于D,∠CBP的平分线交CE于Q,当EP+BP=18时,则CQ的值为查看答案和解析>>
科目:初中数学 来源: 题型:
 如图所示的转盘,分成三个相同的扇形,指针位置固定,转动转盘后任其自由停止,其中的某个扇形会恰好停在指针所指的位置,并相应得到一个数(指针指向两个扇形的交线时,视为无效,重新转动一次转盘),此过程称为一次操作.请用树状图或列表法,求事件“两次操作,第一次操作得到的数与第二次操作得到的数的绝对值相等”发生的概率.
如图所示的转盘,分成三个相同的扇形,指针位置固定,转动转盘后任其自由停止,其中的某个扇形会恰好停在指针所指的位置,并相应得到一个数(指针指向两个扇形的交线时,视为无效,重新转动一次转盘),此过程称为一次操作.请用树状图或列表法,求事件“两次操作,第一次操作得到的数与第二次操作得到的数的绝对值相等”发生的概率.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com