
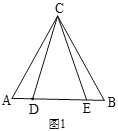
【题目】基础探究:如图1,在,![]() 中,
中,![]() ,
,![]() ,点
,点![]() 、
、![]() 都在边
都在边![]() 上,且
上,且![]() ,连接
,连接![]() 、
、![]() .
.
(1)求证:![]() .
.
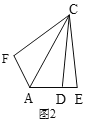
(2)如图2,以![]() 为对角线的四边形
为对角线的四边形![]() 中,
中,![]() ,
,![]() ,将
,将![]() 沿
沿![]() 折叠,得到
折叠,得到![]() ,点
,点![]() 的对应点
的对应点![]() 恰好落在
恰好落在![]() 边上,若
边上,若![]() ,
,![]() ,则四边形
,则四边形![]() 的面积为________.
的面积为________.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)由AC=AB,∠CAB=60°可证明△ABC是等边三角形,可得∠A=∠B=60°,CA=CB,利用SAS可证明△CAD≌△CBE,可得CD=CE,根据等腰三角形的性质即可得出∠CDE=∠CED;
(2)如图,过点A作CB⊥AE于B,根据折叠的性质可得△ACF≌△ACD,可得CF=CD,∠DAC=∠FAC=60°,S△ACF=S△ACD,根据等腰三角形“三线合一”的性质可得BD=![]() DE=
DE=![]() ,可得AB的长,利用∠DAC的三角函数可求出CB的长,根据S四边形AECF= 2S△ACD+S△ADE即可得答案.
,可得AB的长,利用∠DAC的三角函数可求出CB的长,根据S四边形AECF= 2S△ACD+S△ADE即可得答案.
(1)![]() ,
,![]()
![]() 是等边三角形
是等边三角形
![]() ,
,![]()
在△CAD和△CBE中,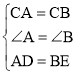 ,
,
∴△CAD≌△CBE,
∴CD=CE,
∴∠CDE=∠CED.
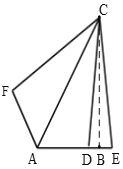
(2)如图,过点C作CB⊥AE于B,
∵将![]() 沿
沿![]() 折叠,得到
折叠,得到![]() ,点
,点![]() 的对应点
的对应点![]() 恰好落在AE边上,
恰好落在AE边上,
∴△ACF≌△ACD,
∴CF=CD,∠DAC=∠FAC=60°,S△ACF=S△ACD,
∵CE=CF,
∴CD=CE,
∵CB⊥DE,DE=1,
∴BD=BE=![]() DE=
DE=![]() ,
,
∵AD=3,
∴AB=AD+BD=![]() ,
,
∴BC=AB·tan∠DAC=![]() ×tan60°=
×tan60°=![]() ,
,
∴S四边形AECF= 2S△ACD+S△ADE=2×![]() AD·BC+
AD·BC+![]() DE·BC=
DE·BC=![]() ,
,
故答案为:![]()


科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=1,∠BAC=45°,△AEF是由△ABC绕点A按顺时针方向旋转得到的.连接BE、CF相交于点D.
(1)求证:BE=CF.
(2)当四边形ACDE为菱形时,求BD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
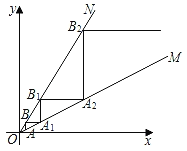
【题目】在平面直角坐标系中,点A(![]() ,1)在射线OM上,点B(
,1)在射线OM上,点B(![]() ,2)在射线ON上,以AB为直角边作Rt△ABA1,以BA1为直角边作第二个Rt△BA1B1,则点B1的纵坐标为_____,然后以A1B1为直角边作第三个Rt△A1B1A2,…,依次规律,得到Rt△B2019A2020B2020,则点B2020的纵坐标为_____.
,2)在射线ON上,以AB为直角边作Rt△ABA1,以BA1为直角边作第二个Rt△BA1B1,则点B1的纵坐标为_____,然后以A1B1为直角边作第三个Rt△A1B1A2,…,依次规律,得到Rt△B2019A2020B2020,则点B2020的纵坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】疫情之下,中华儿女共抗时艰.重庆和湖北同饮长江水,为更好地驰援武汉,打赢防疫攻坚战,我市某公益组织收集社会捐献物资.甲、乙两人先后从![]() 地沿相同路线出发徒步前往
地沿相同路线出发徒步前往![]() 地进行物资捐献,甲出发1分钟后乙再出发,一段时间后乙追上甲,这时甲发现有东西落在
地进行物资捐献,甲出发1分钟后乙再出发,一段时间后乙追上甲,这时甲发现有东西落在![]() 地,于是原路原速返回
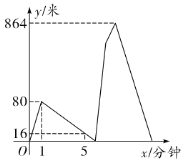
地,于是原路原速返回![]() 地去取(甲取东西的时间忽略不计),而乙继续前行,甲乙两人到达B地后原地帮忙.已知在整个过程中,甲乙均保持各自的速度匀速行走,甲、乙两人相距的路程
地去取(甲取东西的时间忽略不计),而乙继续前行,甲乙两人到达B地后原地帮忙.已知在整个过程中,甲乙均保持各自的速度匀速行走,甲、乙两人相距的路程![]() (米)与甲出发的时间
(米)与甲出发的时间![]() (分钟)之间的函数关系如图所示,则当乙到达
(分钟)之间的函数关系如图所示,则当乙到达![]() 地时,甲距
地时,甲距![]() 地的路程是_______米.
地的路程是_______米.
查看答案和解析>>
科目:初中数学 来源: 题型:
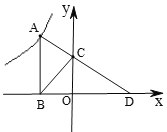
【题目】如图,点![]() 是反比例函数
是反比例函数![]() 的图象上的一点,过点
的图象上的一点,过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() .点
.点![]() 为
为![]() 轴正半轴上的一点,连接
轴正半轴上的一点,连接![]() 、
、![]() ,延长
,延长![]() 交
交![]() 轴于点
轴于点![]() .若
.若![]() ,且
,且![]() 的面积为18,则
的面积为18,则![]() 的值是( )
的值是( )
A.6B.-6C.12D.-12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,将
,将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 后得到
后得到![]() ,将线段
,将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 后得到线段
后得到线段![]() ,分別以
,分別以![]() 、
、![]() 为圆心,
为圆心,![]() 、
、![]() 长为半径画弧
长为半径画弧![]() 和弧
和弧![]() ,连接
,连接![]() ,则图中阴影部分的面积是________.
,则图中阴影部分的面积是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着科技的进步和网络资源的丰富,在线学习已经成为更多人的自主学习选择.某校计划为学生提供以下四类在线学习方式:在线阅读、在线听课、在线答题和在线讨论.为了解学生需求,该校随机对本校部分学生进行了“你对哪类在线学习方式最感兴趣”的调查,并根据调查结果绘制成如下两幅不完整的统计图.
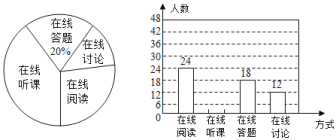
(1)求本次调查的学生总人数,并补全条形统计图;
(2)求扇形统计图中“在线讨论”对应的扇形圆心角的度数;
(3)该校共有学生2100人,请你估计该校对在线阅读最感兴趣的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某同学报名参加校运动会,有以下5个项目可供选择:径赛项目:100m,200m,![]() 分别用
分别用![]() 、
、![]() 、
、![]() 表示
表示![]() ;田赛项目:跳远,跳高
;田赛项目:跳远,跳高![]() 分别用
分别用![]() 、
、![]() 表示
表示![]() .
.
![]() 该同学从5个项目中任选一个,恰好是田赛项目的概率为______;
该同学从5个项目中任选一个,恰好是田赛项目的概率为______;
![]() 该同学从5个项目中任选两个,利用树状图或表格列举出所有可能出现的结果,并求恰好是一个田赛项目和一个径赛项目的概率.
该同学从5个项目中任选两个,利用树状图或表格列举出所有可能出现的结果,并求恰好是一个田赛项目和一个径赛项目的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com