
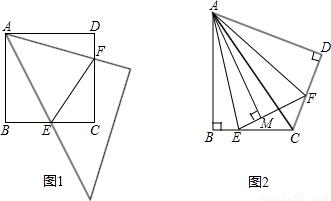
如图1,等腰直角三角板的一个锐角顶点与正方形ABCD的顶点A重合,将此三角板绕点A旋转,使三角板中该锐角的两条边分别交正方形的两边BC,DC于点E,F,连接EF.
(1)猜想BE、EF、DF三条线段之间的数量关系,并证明你的猜想;
(2)在图1中,过点A作AM⊥EF于点M,请直接写出AM和AB的数量关系;
(3)如图2,将Rt△ABC沿斜边AC翻折得到Rt△ADC,E,F分别是BC,CD边上的点,∠EAF=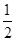 ∠BAD,连接EF,过点A作AM⊥EF于点M,试猜想AM与AB之间的数量关系.并证明你的猜想.
∠BAD,连接EF,过点A作AM⊥EF于点M,试猜想AM与AB之间的数量关系.并证明你的猜想.
(1)EF=BE+DF见解析 (2)AM=AB见解析 (3)AM=AB见解析
【解析】(1)EF=BE+DF,
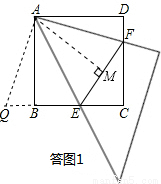
证明:如答图1,延长CB到Q,使BQ=DF,连接AQ,
∵四边形ABCD是正方形,
∴AD=AB,∠D=∠DAB=∠ABE=∠ABQ=90°,
在△ADF和△ABQ中
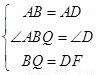
∴△ADF≌△ABQ(SAS),
∴AQ=AF,∠QAB=∠DAF,
∵∠DAB=90°,∠FAE=45°,
∴∠DAF+∠BAE=45°,
∴∠BAE+∠BAQ=45°,
即∠EAQ=∠FAE,
在△EAQ和△EAF中
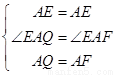
∴△EAQ≌△EAF,
∴EF=EQ=BE+BQ=BE+DF.
(2)【解析】
AM=AB,
理由是:∵△EAQ≌△EAF,
∴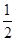 ×EQ×AB=
×EQ×AB=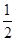 ×FE×AM,
×FE×AM,
又∵EF=EQ,
∴AM=AB.
(3)AM=AB,
证明:如答图2,延长CB到Q,使BQ=DF,连接AQ,

∵折叠后B和D重合,
∴AD=AB,∠D=∠ABE=90°,∠BAC=∠DAC=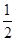 ∠BAD,
∠BAD,
在△ADF和△ABQ中,
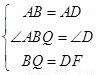
∴△ADF≌△ABQ(SAS),
∴AQ=AF,∠QAB=∠DAF,
∵∠FAE=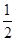 ∠BAD,
∠BAD,
∴∠DAF+∠BAE=∠BAE+∠BAQ=∠EAQ=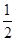 ∠BAD,
∠BAD,
即∠EAQ=∠FAE,
在△EAQ和△EAF中,
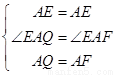
∴△EAQ≌△EAF(SAS),
∴EF=EQ,
∵△EAQ≌△EAF,EF=EQ,
∴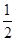 ×EQ×AB=
×EQ×AB=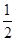 ×FE×AM,
×FE×AM,
∴AM=AB.
(1)延长CB到Q,使BQ=DF,连接AQ,根据四边形ABCD是正方形求出AD=AB,∠D=∠DAB=∠ABE=∠ABQ=90°,证△ADF≌△ABQ,推出AQ=AF,∠QAB=∠DAF,求出∠EAQ=∠F,证△EAQ≌△EAF,推出EF=BQ即可;
(2)根据△EAQ≌△EAF,EF=BQ得出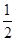 ×BQ×AB=
×BQ×AB=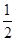 ×FE×AM,求出即可;
×FE×AM,求出即可;
(3)延长CB到Q,使BQ=DF,连接AQ,根据折叠和已知得出AD=AB,∠D=∠ABE=90°,∠BAC=∠DAC=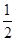 ∠BAD,证△ADF≌△ABQ,推出AQ=AF,∠QAB=∠DAF,求出∠EAQ=∠FAE,证明EAQ≌△EAF,推出EF=EQ即可.
∠BAD,证△ADF≌△ABQ,推出AQ=AF,∠QAB=∠DAF,求出∠EAQ=∠FAE,证明EAQ≌△EAF,推出EF=EQ即可.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2014中考名师推荐数学图形的相似(解析版) 题型:填空题
如图,正方形ABCD的边长为4,E、F分别是BC、CD上的两个动点,且AE⊥EF.则AF的最小值是____________.

查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学图形与坐标(解析版) 题型:填空题
如图,把“QQ”笑脸放在直角坐标系中,已知左眼A的坐标是(-2,3),嘴唇C点的坐标为(-1,1),则将此“QQ”笑脸向右平移3个单位后,右眼B的坐标是 .

查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学反比例函数(解析版) 题型:选择题
已知点A(1,y1)、B(2,y2)、C(-3,y3)都在反比例函数y=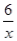 的图象上,则y1、y2、y3的大小关系是( )
的图象上,则y1、y2、y3的大小关系是( )
A.y3<y1<y2
B.y1<y2<y3
C.y2<y1<y3
D.y3<y2<y1
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学分类讨论思想(解析版) 题型:选择题
CD是⊙O的一条弦,作直径AB,使AB⊥CD,垂足为E,若AB=10,CD=8,则BE的长是( )
A.8
B.2
C.2或8
D.3或7
查看答案和解析>>
科目:初中数学 来源:2014中考名师推荐数学三角形(一)(解析版) 题型:填空题
将一副直角三角板如图摆放,点C在EF上,AC经过点D.已知∠A=∠EDF=90°,AB=AC.∠E=30°,∠BCE=40°,则∠CDF= .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com