
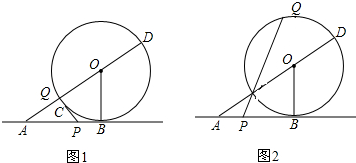
���� ��1����ͼ1���������ߵ����ʿɵá�ACP=90�㣬ֻ�����AC��Ȼ����Rt��ACP���������Ǻ����Ϳɽ�����⣻
��2���õ�Q��CD�ľ���Ϊ$\frac{1}{2}$�����ͼ��2�����ɽ�����⣻
��3������Q��QN��CD��N������P��PM��CD��M������QD����ͼ3����֤��CNQ�ס�QND���������������ε����ʿ����CN����֤��PMC�ס�QNC���������������ε����ʿɵ�PM��CM֮��Ĺ�ϵ���ɡ�MAP=30�㼴�ɵõ�PM��AM֮��Ĺ�ϵ��Ȼ�����AC=AM+CM�Ϳɵõ�PM��ֵ�����ɵõ�AP��ֵ��
��� �⣺��1����AB���O�����ڵ�B�����ABO=90�㣮
�ߡ�DAB=30�㣬OB=$\frac{1}{2}$CD=$\frac{1}{2}$��2=1��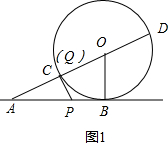
��AO=2OB=2��AC=AO-CO=2-1=1��
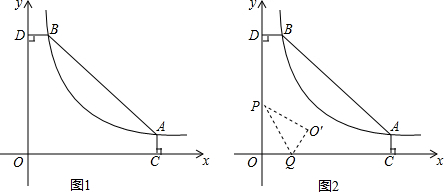
��Q��C�����غ�ʱ��CP���O�����ڵ�C����ͼ1��
���С�ACP=90�㣬
��cos��CAP=$\frac{AC}{AP}$=$\frac{1}{AP}$=$\frac{\sqrt{3}}{2}$��
���AP=$\frac{2\sqrt{3}}{3}$��
��2����4��λ��ʹ��CQD�����Ϊ$\frac{1}{2}$��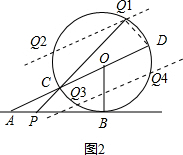
��ʾ�����Q��CD�ľ���Ϊh��
��S��CQD=$\frac{1}{2}$CD•h=$\frac{1}{2}$��2��h=$\frac{1}{2}$��
��h=$\frac{1}{2}$��
����h=$\frac{1}{2}$��1�����ͼ2�ɵã�
��4��λ��ʹ��CQD�����Ϊ$\frac{1}{2}$��
��3������Q��QN��CD��N������P��PM��CD��M����ͼ3��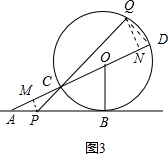 ��S��CQD=$\frac{1}{2}$CD•QN=$\frac{1}{2}$��2��QN=$\frac{1}{2}$����QN=$\frac{1}{2}$��
��S��CQD=$\frac{1}{2}$CD•QN=$\frac{1}{2}$��2��QN=$\frac{1}{2}$����QN=$\frac{1}{2}$��
��CD�ǡ�O��ֱ����QN��CD��
���CQD=��QND=��QNC=90�㣬
���CQN=90��-��NQD=��NDQ��
���QNC�ס�DNQ��
��$\frac{QN}{DN}$=$\frac{NC}{NQ}$��
��QN2=CN•DN��
��CN=x������$\frac{1}{4}$=x��2-x����
������4x2-8x+1=0��
��ã�x1=$\frac{2-\sqrt{3}}{2}$��x2=$\frac{2+\sqrt{3}}{2}$��
��CQ��QD����x=$\frac{2+\sqrt{3}}{2}$��
��$\frac{NC}{QN}$=2+$\sqrt{3}$��
��QN��CD��PM��CD��
���PMC=��QNC=90�㣮
�ߡ�MCP=��NCQ��
���PMC�ס�QNC��
��$\frac{MC}{MP}$=$\frac{NC}{NQ}$=2+$\sqrt{3}$��
��MC=��2+$\sqrt{3}$��MP��
��Rt��AMP��
tan��MAP=$\frac{MP}{AM}$=tan30��=$\frac{\sqrt{3}}{3}$��
��AM=$\sqrt{3}$MP��
��AC=AM+MC=$\sqrt{3}$MP+��2+$\sqrt{3}$��MP=1��
��MP=$\frac{\sqrt{3}-1}{4}$��
��AP=2MP=$\frac{\sqrt{3}-1}{2}$��
���� ������Ҫ���������������ε��ж������ʡ�Բ�ܽǶ��������Ǻ���������ǵ����Ǻ���ֵ�����ߵ����ʡ���һԪ���η��̵�֪ʶ������AP��ֵת��Ϊ���ABC�ǽ���ڣ�3��С��Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{��-2��^{2}}$=-2 | B�� | ��a2��5=a10 | C�� | a2+a5=a7 | D�� | 6$\sqrt{5}$��2$\sqrt{5}$=12$\sqrt{5}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3 | B�� | 0 | C�� | -3 | D�� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ������x�Ķ��κ���y=ax2+bx+c��a��0��c��0��a��b��c�dz�������x�ύ��������ͬ�ĵ�A��x1��0����B��x2��0����0��x1��x2������y�ύ�ڵ�P����ͼ��Ϊ��M����OΪ����ԭ�㣮
������x�Ķ��κ���y=ax2+bx+c��a��0��c��0��a��b��c�dz�������x�ύ��������ͬ�ĵ�A��x1��0����B��x2��0����0��x1��x2������y�ύ�ڵ�P����ͼ��Ϊ��M����OΪ����ԭ�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com