
【题目】如图,已知直线l与⊙O相离,OA⊥l于点A,OA=5,OA⊙O相交于点P,AB与⊙O相切于点B,BP的延长线交直线l于点C.
(1)试判断线段AB与AC的数量关系,并说明理由;
(2)若 ![]() ,求⊙O的半径和线段PB的长.
,求⊙O的半径和线段PB的长.
【答案】
(1)解:AB=AC,理由如下:
连接OB.
∵AB切⊙O于B,OA⊥AC,
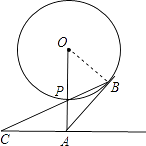
∴∠OBA=∠OAC=90°,
∴∠OBP+∠ABP=90°,∠ACP+∠APC=90°,
∵OP=OB,
∴∠OBP=∠OPB,
∵∠OPB=∠APC,
∴∠ACP=∠ABC,
∴AB=AC;
(2)解:延长AP交⊙O于D,连接BD,

设圆半径为r,则OP=OB=r,PA=5﹣r,
则AB2=OA2﹣OB2=52﹣r2,
AC2=PC2﹣PA2=(2 ![]() )2﹣(5﹣r)2,
)2﹣(5﹣r)2,
∴52﹣r2=(2 ![]() )2﹣(5﹣r)2,
)2﹣(5﹣r)2,
解得:r=3,
∴AB=AC=4,
∵PD是直径,
∴∠PBD=90°=∠PAC,
又∵∠DPB=∠CPA,
∴△DPB∽△CPA,
∴ ![]() ,
,
∴ ![]() ,
,
∴BP= ![]() ,
,
答:圆的半径是3,线段PB的长为 ![]() .
.
【解析】(1)连接OB,根据切线的性质和垂直得出∠OBA=∠OAC=90°,得出∠OBP+∠ABP=90°,∠ACP+∠CPA=90°,求出∠ACP=∠ABC,根据等腰三角形的判定推出即可。
(2)延长AP交 O于D,连接BD,设圆半径为r,则OP=OB=r,PA=5-r,根据AB=AC,建立方程求出t的值,再证明△DPB∽△CPA,得出对应边成比例,求出BP的长。


科目:初中数学 来源: 题型:
【题目】计算题
(1)计算:(3﹣π)0+(﹣ ![]() )﹣2+
)﹣2+ ![]() ﹣2|sin45°﹣1|;
﹣2|sin45°﹣1|;
(2)先化简,再求值: ![]() ,其中实数m使关于x的一元二次方程x2﹣4x﹣m=0有两个相等的实数根.
,其中实数m使关于x的一元二次方程x2﹣4x﹣m=0有两个相等的实数根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为深化义务教育课程改革,满足学生的个性化学习需求,某校就“学生对知识拓展、体育特长、艺术特长和时间活动四类选课意向”进行了抽样调查(每人选报一类),绘制了如图所示的两幅统计图(不完整),请根据图中信息,解答下列问题.


(1)求扇形统计图中的m的值,并补全条形统计图;
(2)已知该校800名学生,计划开设“实践活动类”课程,每班安排20人,问学校开设多少个“实践活动课”课程的班级比较合理.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某园艺公司对一块直角三角形的花圃进行改造,测得两直角边长为6m、8m.现要将其扩建成等腰三角形,且扩充部分是以8m为直角边的直角三角形.求扩建后的等腰三角形花圃的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,EF∥AD,∠1=∠2.证明:∠DGA+∠BAC=180°.请完成说明过程.
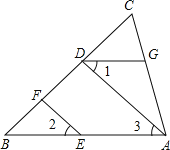
解:∵EF∥AD,(已知)
∴∠2=∠3.( )
又∵∠1=∠2(已知)
∴∠1=∠3,(等量代换)
∴AB∥ ,( )
∴∠DGA+∠BAC=180°.( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,AB=AC,点D为BC中点.∠MDN=90°,∠MDN绕点D旋转,DM、DN分别与边AB、AC交于E、F两点.下列结论:
①△DEF是等腰直角三角形;
②AE=CF;
③△BDE≌△ADF;
④BE+CF=EF;
⑤S四边形AEDF=![]() AD2,
AD2,
其中正确结论是_____(填序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李红在学校的研究性学习小组中负责了解初一年级200名女生掷实心球的测试成绩.她从中随机调查了若干名女生的测试成绩(单位:米),并将统计结果绘制成了如下的统计图表(内容不完整).
测试成绩 |
|
|
|
|
| 合计 |
频数 | 3 | 27 | 9 | m | 1 | n |
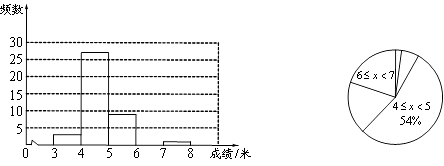
请你结合图表中所提供的信息,回答下列问题:
(1)表中m= , n=;
(2)请补全频数分布直方图;
(3)在扇形统计图中, ![]() 这一组所占圆心角的度数为度;
这一组所占圆心角的度数为度;
(4)如果掷实心球的成绩达到6米或6米以上为优秀,请你估计该校初一年级女生掷实心球的成绩达到优秀的总人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com