练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    20．将图①中的正方形剪开得到图②，图②中共有4个正方形；将图②中一个正方形剪开得到图③，图③中共有7个正方形；将图③中一个正方形剪开得到图④，图④中共有10个正方形…如此下去，则第2016个图中共有正方形的个数为（　　）
    A．2016B．2019C．6046D．6050

    分析 观察图形可知，每剪开一次多出3个正方形，然后写出前4个图形中正方形的个数，再根据此规律写出第n个图形中的正方形的个数的表达式即可．

    解答 解：第1个图形有正方形1个，
    第2个图形有正方形4个，
    第3个图形有正方形7个，
    第4个图形有正方形11个，
    …，
    第n个图形有正方形（3n-2）个，
    当n=2016时，3×2016-2=6046个正方形，
    故选C．
    故答案为：（3n-2）．

    点评 本题是对图形变化规律的考查，观察出每剪开一次多出3个正方形是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    10．已知（-3，y1），（0，y2），（3，y3）是抛物线y=-3x2+6x-k上的点，则（　　）
    A．y1＜y2＜y3B．y1＜y3＜y2C．y3＜y1＜y2D．y2＜y1＜y3

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    11．如图，菱形OBCD在平面直角坐标系中的位置如图所示，顶点B（0，2$\sqrt{3}$），∠DOB=60°，点P是对角线OC上的一个动点，已知A（-1，0），则AP+BP的最小值为（　　）
    A．4B．5C．3$\sqrt{3}$D．$\sqrt{19}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．若|m+5|=4，|n|=6，|m-n|=n-m，求mn-（m+n）的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    15．已知抛物线y1=-$\frac{2}{3}$（x+1）2，则与抛物线y1关于y轴对称的抛物线y2的函数表达式为y2=-$\frac{2}{3}$（x-1）2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．在平面直角坐标系xOy中，对于任意两点P1（x1，y1）与P2（x2，y2）的“非常距离”，给出如下定义：
    若|x1-x2|≥|y1-y2|，则点P1与点P2的“非常距离”为|x1-x2|；
    若|x1-x2|＜|y1-y2|，则点P1与点P2的“非常距离”为|y1-y2|．
    例如：点P1（1，2），点P2（3，5），因为|1-3|＜|2-5|，所以点P1与点P2的“非常距离”为|2-5|=3，也就是图1中线段P1Q与线段P2Q长度的较大值（点Q为垂直于y轴的直线P1Q与垂直于x轴的直线P2Q交点）．

    （1）已知点A（0，1），B为y轴上的一个动点，
    ①若点A与点B的“非常距离”为3，写出一个满足条件的点B的坐标；
    ②直接写出点A与点B的“非常距离”的最小值；
    （2）已知M是直线y=-$\frac{1}{2}$x-2上的一个动点，
    ①如图2，点N的坐标是（-2，0），求点M与点N的“非常距离”d的最小值及相应的点M的坐标；
    ②若P是坐标平面内的一个动点，且OP=$\frac{\sqrt{5}}{2}$，直接写出点M与点P的“非常距离”d的最小值及相应的点P和点M的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

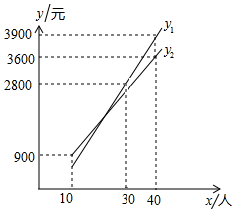    8．2016年3月28日，农业部发布了以“早春到乡村去踏青”为主题的219条休闲农业精品景点线路，其中河北省的“唐山迁西滨水度假游”等20条休闲农业精品线路入选．已知河北省某旅游景点的门票为a元/人，为吸引团队游客，对团队10人以上（包含10人）的游客实行动态票价：节假日期间门票不打折，但会在团队总费用的基础上有优惠；非节假日期间门票打b折．某团队在节假日期间的门票总费用y1（元）、非节假日期间的门票总费用y2（元）与团队人数x（人）（x≥10）之间的函数关系的图象如图所示．
    （1）求y1、y2与x之间的函数解析式；
    （2）“五一“期间，张恒和朋友们去该旅游景点游玩，他们共花费门票710元，求他们共去了几人？
    （3）河北春秋旅行社组织老年团队去该旅游景点，他们选择什么时间去比较合算？

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    5．若方程组$\left\{\begin{array}{l}x+y=m+1\\ 2x+y=3\end{array}\right.$中，若未知数x、y满足x+y＞5，则m的取值范围是（　　）
    A．m≥-4B．m＞4C．m＜-4D．m≤-4

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    6．图中为轴对称图形的是（　　）
    A．（1 ）（2）B．（1）（4）C．（2）（3）D．（3）（4）

    查看答案和解析>>

    同步练习册答案