
【题目】如图,△ABC的边BC在直线l上,AD是△ABC的高,∠ABC=45°,BC=6cm,AB=2![]() cm.点P从点B出发沿BC方向以1cm/s速度向点C运动,当点P到点C时,停止运动.PQ⊥BC,PQ交AB或AC于点Q,以PQ为一边向右侧作矩形PQRS,PS=2PQ.矩形PQRS与△ABC的重叠部分的面积为S(cm2),点P的运动时间为t(s).回答下列问题:
cm.点P从点B出发沿BC方向以1cm/s速度向点C运动,当点P到点C时,停止运动.PQ⊥BC,PQ交AB或AC于点Q,以PQ为一边向右侧作矩形PQRS,PS=2PQ.矩形PQRS与△ABC的重叠部分的面积为S(cm2),点P的运动时间为t(s).回答下列问题:
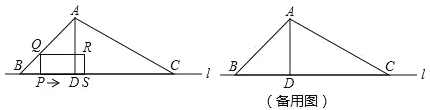
(1)AD= cm;
(2)当点R在边AC上时,求t的值;
(3)求S与t之间的函数关系式.
【答案】(1)2;(2)![]() ;(3)①当0<t≤
;(3)①当0<t≤![]() 时,S= 2t2.②当
时,S= 2t2.②当![]() <t<2时,S=-
<t<2时,S=-![]() t2+15t-9.
t2+15t-9.
③当2≤t<6时,S=![]() t2-3t+9.
t2-3t+9.
【解析】
试题分析:(1)由AD是△ABC的高,∠ABC=45°,可得AD=BD,再由AB=2![]() cm,即可得出AD的长;
cm,即可得出AD的长;
(2)根据QR∥BC,可证明△AQR∽△ABC,从而得出![]() ,即
,即![]() ,解得t即可;
,解得t即可;
(3)分三段进行讨论:
①当0<t≤![]() 时(图1),根据∠B=45°,∠BPQ=90°,即可得出∠BQP=45°,则PQ=BP=t,从而得出S与t之间的函数关系式;
时(图1),根据∠B=45°,∠BPQ=90°,即可得出∠BQP=45°,则PQ=BP=t,从而得出S与t之间的函数关系式;
②当![]() <t<2时(图2),根据∠BAD=45°,则BD=AD=2cm,从而得出CD,即可证明△FSC∽△ADC,得比例式
<t<2时(图2),根据∠BAD=45°,则BD=AD=2cm,从而得出CD,即可证明△FSC∽△ADC,得比例式![]() ,则SF=3-
,则SF=3-![]() t,再求得FR,由ER∥SC,得∠REF=∠C,即可证明△ERF∽△CDA,则
t,再求得FR,由ER∥SC,得∠REF=∠C,即可证明△ERF∽△CDA,则![]() ,ER=5t-6,从而得出S与t之间的函数关系式;
,ER=5t-6,从而得出S与t之间的函数关系式;
③当2≤t<6时(图3),根据PQ∥AD,得△ERF∽△CDA,则![]() ,即
,即![]() ,得出QP=3-
,得出QP=3-![]() t,从而得出S与t之间的函数关系式.
t,从而得出S与t之间的函数关系式.
试题解析:(1)∵AD是△ABC的高,
∴∠ADB=90°,
∵∠ABC=45°,
∴AD=BD,
∵AB=2![]() cm,
cm,
∴AD=2cm,
(2)∵QR∥BC,
∴△AQR∽△ABC,
∴![]() ,即
,即![]() ,
,
解得,t=![]() ;
;
(3)①当0<t≤![]() 时(图1),∠B=45°,∠BPQ=90°,
时(图1),∠B=45°,∠BPQ=90°,
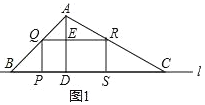
∴∠BQP=90°-45°=45°
∴PQ=BP=t
∴S=S矩形PQRS=2tt=2t2.
②当![]() <t<2时(图2)∠BAD=90°-45°=45°
<t<2时(图2)∠BAD=90°-45°=45°

BD=AD=2cm
CD=6-2=4cm.
SF∥AD
∴△FSC∽△ADC
∴![]() ,即
,即![]() ,
,
SF=3-![]() t,
t,
∴FR=t-(3-![]() t)=
t)=![]() -3,
-3,
∵ER∥SC,
∴∠REF=∠C
又∠REF=∠ADC=90°
∴△ERF∽△CDA
∴![]() ,
,
即 ,
,
ER=5t-6,
∴S=S矩形PQRS-S△ERF=2t2-![]() (5t-6)(
(5t-6)(![]() t-3)
t-3)
=-![]() t2+15t-9.
t2+15t-9.
③当2≤t<6时(图3)

∵PQ∥AD
∴△ERF∽△CDA,
∴![]() ,
,
即![]() ,
,
∴QP=3-![]() t
t
∴S=S△QPC=![]() (3-
(3-![]() t)(6-t)
t)(6-t)
=![]() t2-3t+9.
t2-3t+9.


科目:初中数学 来源: 题型:
【题目】⊙O 的直径 AB 长为 10,弦 MN⊥AB,将⊙O 沿 MN 翻折,翻折后点 B 的对应点为点 B′,若 AB′=2,MB′的长为( )
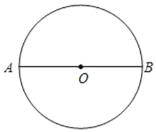
A. 2 ![]() B. 2
B. 2![]() 或 2
或 2![]() C. 2
C. 2![]() D. 2
D. 2 ![]() 或 2
或 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在菱形ABCD中, BE⊥AD于点E,延长AD至F,使DF=AE,连接CF.
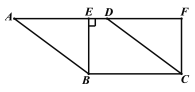
(1)判断四边形EBCF的形状,并证明;
(2)若AF=9,CF=3,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
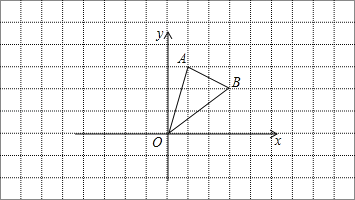
【题目】如图,在边长为1的小正方形网格中,△AOB的顶点均在格点上,
(1)B点关于y轴的对称点坐标为 ;
(2)将△AOB向左平移3个单位长度得到△A1O1B1,请画出△A1O1B1;
(3)以原点O为对称中心,画出△ AOB与关于原点对称的△ A2 O B2;
(4)以原点O为旋转中心,画出把△AOB顺时针旋转90°的图形△A3 O B3.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两台机床同时加工直径为![]() 的同种规格零件,为了检查两台机床加工零件的稳定性,质检员从两台机床的产品中各抽取
的同种规格零件,为了检查两台机床加工零件的稳定性,质检员从两台机床的产品中各抽取![]() 件进行检测,结果如下(单位:
件进行检测,结果如下(单位:![]() ):
):
甲 |
|
|
|
|
|
乙 |
|
|
|
|
|
(1)分别求出这两台机床所加工零件直径的平均数和方差;
(2)根据所学的统计知识,你认为哪一台机床生产零件的稳定性更好一些,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中每个小正方形的边长都是1个单位长度,Rt△ABC的三个顶点A(-2,2),B(0,5),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,得到△A1B1C,请画出△A1B1C的图形.
(2)平移△ABC,使点A的对应点A2坐标为(-2,-6),请画出平移后对应的△A2B2C2的图形.
(3)若将△A1B1C绕某一点旋转可得到△A2B2C2,请直接写出旋转中心的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=xm.
(1)若花园的面积为192m2, 求x的值;
(2)若在P处有一棵树与墙CD,AD的距离分别是15m和6m,要将这棵树围在花园内(含边界,不考虑树的粗细),求花园面积S的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋子中装有三个完全相同的小球,分别标有数字3、4、5.从袋子中随机取出一个小球,用小球上的数字作为十位的数字,然后放回;再取出一个小球,用小球上的数字作为个位上的数字,这样组成一个两位数,试问:按这种方法能组成哪些位数?十位上的数字与个位上的数字之和为9的两位数的概率是多少?用列表法或画树状图法加以说明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com